Re: Een kubus

Dit is een reactie op vraag 88967

Hi, ik heb de vlakken van y=3 en z=1 getekend en een vectorvoorstelling van het vlak z=1 in OCGF opgesteld.

Ik snap niet wat ze bedoelen met de dragers van DG. Ik zie in het antwoord heel andere soort antwoorden.

mboudd
Leerling mbo - woensdag 8 januari 2020

Antwoord

Ze lijn $z=1$ ligt in vlak $OCFG$.



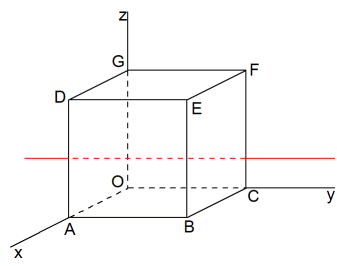
Voor een vectorvoorstelling heb je een steun- en een richtingsvector nodig. Je neemt als steunvector (0,0,1). Dat is prima. De richtingsvector wordt dan bijvoorbeeld (0,1,0). Ga maar na!

Nu zijn er natuurlijk nog heel veel meer antwoorden mogelijk, maar deze ligt het meest voor de hand:

$
\left( {\begin{array}{*{20}c}
x \\
y \\
z \\
\end{array}} \right) = \left( {\begin{array}{*{20}c}
0 \\
0 \\
1 \\
\end{array}} \right) + \lambda \left( {\begin{array}{*{20}c}
0 \\
1 \\
0 \\
\end{array}} \right)
$

Een drager is de lijn die door een lijnstuk loopt. De drager van $DG$ is dan de lijn door de punten $D$ en $G$. Kies weer een steun- en een richtingsvector. Er zijn weer heel veel mogelijkheden maar ik zou deze nemen:

$
\left( {\begin{array}{*{20}c}
x \\
y \\
z \\
\end{array}} \right) = \left( {\begin{array}{*{20}c}
0 \\
0 \\
6 \\
\end{array}} \right) + \lambda \left( {\begin{array}{*{20}c}
1 \\
0 \\
0 \\
\end{array}} \right)
$

Zoals gezegd zijn er meerdere goede antwoorden mogelijk. Zorg ervoor dat je steunvector op de lijn ligt en dat de richtingsvector op een factor na hetzelfde is als bij het antwoord.

Succes!

woensdag 8 januari 2020

©2001-2024 WisFaq