Meetkunde, bewijzen straal cirkel

Hoi, ik heb een vraag over meetkunde in het onderwerp bewijzen. Ik kreeg als huiswerkopgave, drie cirkels waarvan ik van 2 de straal wist maar van de derde cirkel niet. Ik zou met Pythagoras de straal moeten berekenen, maar ik weet niet helemaal hoe ze dat hebben gedaan.
gegeven is dat:

c₁: Middelpunt (0,4) en r = 4
c₂: r = 2 en die de x-as raakt en ook cirkel 1
c₃: raakt c₁ en c₂ en de x-as

Ik moest bewijzen door de pythagorasmethode dat ik op een straal van 4√2 kwam.

Kunt u mij alstublieft helpen?

Ela
Leerling bovenbouw havo-vwo - vrijdag 29 november 2019

Antwoord

Hallo Ela,

Als ik het goed begrijp, gaat het om de volgende figuur:



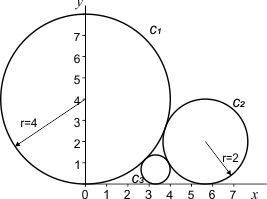
Als dit inderdaad is wat je bedoelt, dan kan de straal van cirkel c₃ niet gelijk zijn aan 4√2.
Hieronder zie je dat ik in de figuur driehoek ABC heb getekend:



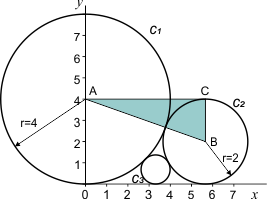
A en B zijn de middelpunten van c₁ en c₂. AC is evenwijdig aan de x-as, BC is evenwijdig aan de y-as. Je ziet: AB=4+2=6 en BC=2. Met pythagoras berekenen we:

AC=√(6²-2²)
AC=√32
AC=4√2

Volgens jou zou de straal van c₃ ook gelijk zijn aan 4√2, maar in de figuur zie je dat deze straal niet gelijk kan zijn aan de zijde AC. Heb je de vraag verkeerd overgenomen, of heb je een tussenresultaat aangezien als eindantwoord?

Ik help je op weg om de straal van c₃ te berekenen, zie de figuur hieronder.



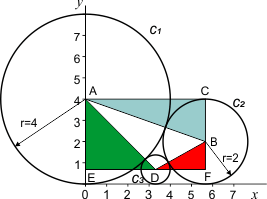
Ik heb nog twee driehoeken toegevoegd. D is het middelpunt van c₃, het lijnstuk EDF is evenwijdig aan de x-as. De straal van c₃ noem ik r.

In driehoek ADE geldt dan:
DE²=AD²-AE²
DE²=(4+r)²-(4-r)²
DE²=16r (vergelijking 1)

In driehoek BDF geldt:
DF²=BD²-BF²
DF²=(2+r)²-(2-r)²
DF²=8r (vergelijking 2)

Verder weet je:
DE+DF=AC)
DE+DF=4√2 (vergelijking 3

Je hebt nu 3 vergelijkingen met 3 onbekenden (DE, DF en r). Hiermee is r te berekenen.

Lukt het hiermee?

vrijdag 29 november 2019

©2001-2024 WisFaq