Correlatie en regressie

Hallo,

Ik heb een opdracht bij de volgende tabel, die ik niet begrijp:

X  12  4   3   4   7   6   8  9  12  10  11  14  12  15  15 
Y  56  53  51  50  46  44  44 42  8  35  30  28  24  22  20 

Ik zal eerst even de gegevens die ik al bij eerdere delen van de opdracht heb gevonden, en die handig zouden kunnen zijn bij het antwoorden van deze vraag:

ik heb de punten van deze tabel al weergegeven in een duidelijke tekening

Ik betrek de punten (12;56) en (12;8) niet bij de verdere berekeningen, omdat die ver buiten de rest van de puntenwolk vallen

Ik heb de pmcc:r al berekend r=-0,966
SD(X)=4,028
SD(Y)=11,222

vergelijking van de regressielijn bij de regressie van Y op X:
^
Y= -2,961X+62,042

vergelijking van de regressielijn bij de regressie van X op Y:
^
X=-0,347Y+22,119

Dat was het wel zo'n beetje.
Nu komt de vraag die ik niet begrijp;

Bereken tussen welke grenzen je X mag verwachten als Y=40

Zouden jullie deze vraag alstjeblieft heel duidelijk stap voor stap uit willen leggen, het is belangrijk en zouden jullie misschien ook zo snel mogelijk willen antwoorden?

Alvast heel erg bedankt!!!
Groetjes Anne

Anne
Leerling bovenbouw havo-vwo - vrijdag 21 maart 2003

Antwoord

Of het weglaten van die twee waarden echt de bedoeling is....
Ik neem aan dat de uitgevoerde berekeningen correct zijn
^
X= -0,347Y + 22,119 voorspelt X uit Y, als nu Y₀=40 waartussen ligt dan X (met 95% zekerheid)

Bereken nu de storingsterm (standaarddeviatie) met:



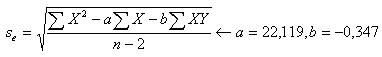
Bereken vervolgens de standaarddeviatie sf voor een voorspelling:



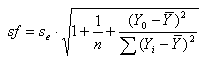
Hierbij is Y₀=40
De grenzen waarde schatting voor X met 95% betrouwbaarheid tussen zal liggen zijn: X_dakje - t·sf en X_dakje + t·sf
Die t waarde komt uit een students T verdeling met n-2 vrijheidsgraden d.w.z. t₁₁=2,20

t'is niet makkelijk maar zou het zo lukken ?

Met vriendelijke groet

JaDeX

zondag 23 maart 2003

©2001-2024 WisFaq