Vlakke meetkunde probleem - IMO-opgave?

In driehoek ABC is AD de bissectrice van hoek A (met D op BC). De punten M en N zijn de projecties van respectievelijk B en C op AD. De cirkel met diameter MN snijdt BC in X en Y.

• Bewijs dat hoek BAX gelijk is aan hoek CAY.

Tot op heden ben ik er niet in geslaagd om dit probleem op te lossen. Wie helpt?

Matthijs

Matthi
Iets anders - zaterdag 15 juni 2019

Antwoord

Beste Matthijs,

De oplossing van het probleem ligt niet direct voor de hand.
Maar collega-beantwoorder TD zette mij op het goede spoor (waarvoor dank, Tom):

Gebruik het harmonisch puntenviertal op een zijde van een driehoek dat bepaald is door de hoekpunten en de voetpunten van de binnen- en buitenbissectrice van de overstaande hoek van die zijde.



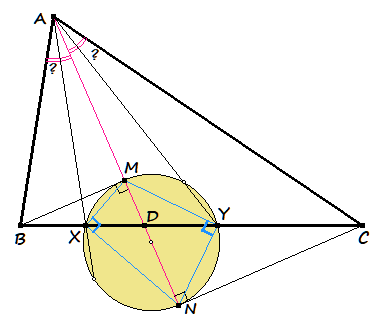
De driehoeken AMB en ANC zijn gelijkvormig (hh), zodat
(1) AM : AN = BM : CN
Dat geldt ook voor BMD en CND, zodat
(2) BM : CN = MD : ND
Uit (1) en (2) volgt dan:
AM : AN = MD : ND of ook MA : MD = NA : ND
Anders geschreven: (MA : MD) : (NA : ND) = 1

Maar dit betekent dat de puntenparen (A, D) en (M, N) harmonische puntenparen zijn; meestal geschreven als (ADMN) = -1.

In driehoek AXD is dan, door de loodrechte stand van MX, NX (Thales-cirkel op MN), de lijn XM de (binnen)bissectrice van hoek X.

Analoog is YM in driehoek AYD de (binnen)bissectrice van hoek Y.

Maar dan is het punt M het snijpunt van twee bissectrices in driehoek AXY, zodat AM bissectrice is van hoek A in die driehoek.

Nu volgt direct de gelijkheid van de twee hoeken die in de figuur met een vraagteken zijn aangegeven.

N.B.
De harmonische verhouding op een zijde van een driehoek volgt direct uit de bissectricestellingen (binnen- en buitenbissectrice).

Zie eventueel lemma 5 in onderstaand pdf-bestand.

Groetend,

Zie IMO-training 2010 (pdf, Engels)

dinsdag 18 juni 2019

©2001-2024 WisFaq