Lotto: winstkansen met elkaar gedeeltelijk overlappende combinaties

Bij de Belgische Lotto worden 6 winnende nummers en 1 bonusnummer getrokken uit een totaal van 45.
Hoe bereken ik mijn kans op 1 winnend nummer + het bonusnummer als ik met volgende combinaties speel:
Comb. A: 1-2-3-4-5-6
Comb. B: 1-2-3-4-7-8

Ik weet dat ik met zowel A als B een kans heb van 1 op 18 (afgerond). Maar samen geven A en B mij geen kans van 2 x 1/18 = 1/9 aangezien 4 nummers uit A ook in B voorkomen. A en B hebben daardoor 6 mogelijke "koppels" met elkaar gemeen: 1-2, 1-3, 1-4, 2-3, 2-4, 3-4.

Als 1 van de 6 gemeenschappelijke koppels wordt getrokken, dan win ik twee keer. Maar daar gaat het mij niet om. Ik speel met slecht 24 in plaats van 30 verschillende koppels. Hoe bereken ik de kans dat 1 van die 24 getrokken wordt?

Luc
Iets anders - zaterdag 23 juni 2018

Antwoord

Hallo Luc,

Laten we de nummers voorstellen als gekleurde knikkers:

nr. 1 t/m 4: rood (4 stuks)
nr. 5 t/m 8: groen (4 stuks)
nr. 9 t/m 45: blauw (37 stuks)

Je wint twee keer wanneer zowel het bonusnummer als het winnende nummer rood is, en de overige vijf nummers blauw.

De kans op een rood bonusnummer is 4/45.

Uit de overige 44 nummers moeten we nog 6 andere nummers kiezen, waarvan 1 rood uit 3 overgebleven rode, en 5 blauw uit 37. We hebben hier te maken met een hypergeometrische verdeling. De gevraagde kans is:



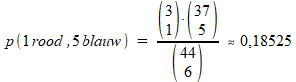
De kans op 2 keer winnen is dan:

(4/45)·0,18525 $\approx$ 0,01647

Op gelijksoortige wijze bereken je de kans dat spel A wint, deze is 0,05438 (afgerond inderdaad ongeveer 1 op 18).
De kans dat je wint, bereken je met:

p(winnen) = p(A wint) + p(B wint) - p(A en B winnen)
p(winnen) = 0,05438 + 0,05438 - 0,01647 $\approx$ 0,0923
(ongeveer 1 op 11).

zaterdag 23 juni 2018

Re: Lotto: winstkansen met elkaar gedeeltelijk overlappende combinaties

©2001-2024 WisFaq