
Verzamelingen
In een klas zitten 22 leerlingen, 10 leerlingen voetballen, 8 leerlingen basketten, 11 leerlingen tennissen, 5 leerlingen voetballen en tennissen, 3 leerlingen voetballen en basketten en 3 leerlingen tennissen en basketten.
a) Hoeveel leerlingen basketten niet ?
b) Hoeveel leerlingen voetballen en tennissen wel maar basketten niet ?
Stel V = verzameling van de leerlingen die voetballen,
B = verzameling van de leerlingen die basketten,
T = verzameling van de leerlingen die tennissen
S = verzameling van alle leerlingen in de klas
Gegeven #S=22, #V=10, #B=8, #T=11,
#(V^T)=5, #(V^B)=3, #(T^B)=3
Antwoord a : Aangezien S = B v (niet B)
geldt #S = #B + #(niet B) =$>$ #(niet B)=22-8=14
Antwoord b : Hier zit ik vast want ik vind het vreemd dat indien ik wil bepalen hoeveel leerlingen er voetballen en tennissen en basketten ik 4 als resultaat bekom.
Aangezien S = B v V v T geldt
#S = #B + #V + #T - #(B^V) - #(B^T) - #(V^T) + #(B^V^T)
22 = 8 + 10 + 11 - 3 - 3 - 5 + #(B^V^T)
=$>$ #(B^V^T) = 22 - 18 = 4
Heel vreemd aangezien #(B^T) = 3 alsook #(B^V) = 3 terwijl deze aantallen in feite toch groter of gelijk zouden moeten zijn aan #(B^V^T)
Is er ergens een foutje in de opgave of zit ik op een volledig verkeerd spoor ?
Alvast bedank voor een antwoord,
Luca
Luca
3de graad ASO - woensdag 23 mei 2018
Antwoord
Hallo Luca,
Volgens mij is er wel iets mis met deze opgave, maar je ziet zelf ook een detail over het hoofd: je gaat ervan uit dat alle leerlingen sporten, maar er kunnen ook leerlingen zijn die geen enkele sport beoefenen (of een andere dan deze drie).
Eerst maar eens vraag a. Deze is snel beanwoord: als 8 leerlingen basketballen, dan blijven er 22-8=14 over die niet basketballen (het doet er niet toe of deze een andere sport uitoefenen of helemaal niet sporten).
Om vraag b aan te pakken, stel ik:
x = het aantal leerlingen dat alledrie de sporten beoefent.
Omdat 5 leerlingen voetballen en tennissen, blijven 5-x leerlingen over die voetballen en tennissen, maar niet basketballen. Op dezelfde wijze kan je bepalen hoeveel leerlingen andere combinaties van twee sporten beoefenen. Handig is om dit weer te geven in een Venn-diagam:
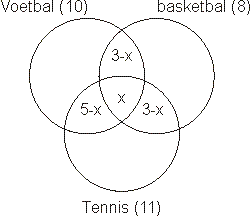
Het aantal leerlngen V dat alleen voetbalt, vind je door de grote cirkel linksboven aan te vullen tot 10:
V + (5-x) + x + (3-x) = 10
V + 8 - x = 10
V = x+2
Op dzelfde wijze vind je het aantal leerlingen dat alleen basketbalt en het aantal dat alleen tennist:
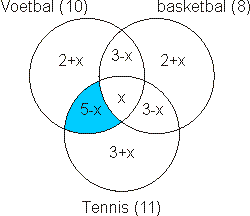
Het totaal aantal sportende leerlingen T vind je door de aantallen in elk vak op te tellen:
T = 2+x + 3-x + 2+x + ... + 3+x
T = 18+x
Wanneer je aanneemt dat alle leerlingen sporten, dus 18+x=22, dan vind je x=4. Maar dat zou de volgende aantallen opleveren:
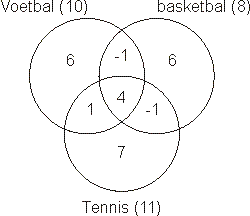
Getalsmatig klopt dit, maar een negatief aantal leerlingen bestaat niet. Met de gegeven randvoorwaarden kan het dus niet zijn dat alle leerlingen sporten. Anders gezegd:
18+x$\le$22
x$\le$4
Er blijven 4-x leerlingen over die niet sporten.
Om in elk vak een niet-negatieve waarde te krijgen, moet gelden:
0$\le$x$\le$3
Bij vraag b wordt het aanal leerlingen in het blauwe vak gevraagd: wel voetbal en tennis (in totaal 5), maar niet tegelijkertijd basketbal (x). Dit aantal is 5-x, dus 2, 3, 4 of 5.

woensdag 23 mei 2018
 ©2001-2024 WisFaq
©2001-2024 WisFaq
|