Grafische methode van Cremona

Beste :),
Ik ben een studente die een voorbereidingscursus thuis volg voor een technische opleiding. Ik loop vast met een vraag over Cremona? Kunt u mij hiermee helpen.

Ontwerp een voetbrugje van 1m breedte dat 15m of meer overspant, het gaat om een vectoractief principe. De last op het dek bedraagt 5kN/m2, verwaarloos het eigengewicht van het brugje. Bepaal de staafkrachten ervan met de grafische methode van Cremona?

Met vriendelijke groeten

ester
Cursist vavo - zondag 20 mei 2018

Antwoord

Hallo Ester,

Stel dat je deze constructie zou kiezen:



Reken dan eerst de verdeelde belasting op het dek om tot krachten op de knooppunten. Bereken ook de ondersteuningskrachten, zodanig dat het geheel in evenwicht is:



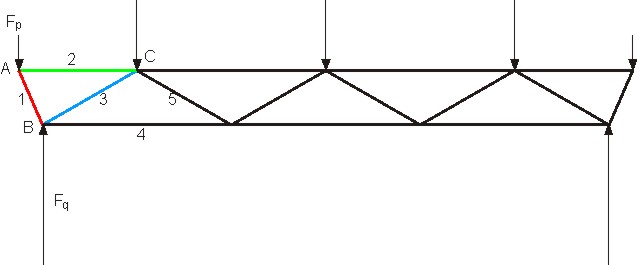
Je start de berekening in een knooppunt waarop hooguit 2 onbekende krachten werken. In dit geval is dit knooppunt A. De belasting op dit punt heb ik F_p genoemd.

Je begint het diagram door vanuit een oorsprong de bekende kracht op dit knooppunt te tekenen. Kies een geschikte schaal. Hier is dit F_p, verticaal naar beneden.

Teken op de kop van F_p een werklijn in de richting van één van de onbekende krachten (hier: in de richting van staaf 1, rood), en vanuit de staart een werklijn in de richting van de tweede onbekende kracht (hier: in de richting van staaf 2, groen):



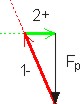
De werklijnen snijden elkaar, hiermee ontstaat een gesloten krachtenveelhoek (hier een driehoek). De zijden van deze driehoek geven de verhoudingen van de drie krachten weer. De richting is zodanig dat de vectoren 'kop op staart' staan.

Ik heb de richting in de figuur getekend, maar straks zal blijken dat dit niet handig is. In plaats daarvan bekijken we of we te maken hebben met trekkrachten of drukkrachten.
In de krachtendriehoek zie je dat staafkracht 1 naar knooppunt A toe gericht is. In staaf 1 heerst dus een drukkracht. Dit geven we aan met een min-teken. De kracht in staaf 2 is van knooppunt A af gericht. Dit is een trekkracht, dit geven we aan met een plus-teken.

Alle krachten op knooppunt A zijn nu bekend, we gaan naar een volgend knooppunt. Dit is knooppunt B. Immers, de kracht in staaf A is inmiddels bekend, de ondersteuningskracht F_q is bekend, dus in knooppunt B zijn maar twee onbekende krachten (in staaf 3 en 4).

We beginnen met het tekenen van de bekende krachten, 'kop op staart'. Ik doe dit hieronder in een aparte figuur, maar je kunt de krachten ook in één complete figuur tekenen (zie Wikipedia: Cremona diagram).

Ik start met de zojuist berekende kracht in staaf 1. Dit is een drukkracht, de kracht is naar knooppunt B toe gericht:



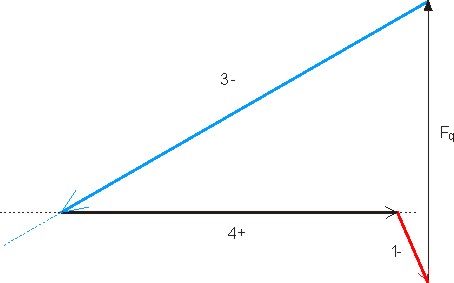
Nu zie je waarom het niet handig is om de pijlpunt te tekenen: op knooppunt A werkte de drukkracht in staaf 1 naar links-boven, maar diezelfde drukkracht werkt op knooppunt B naar rechts-onder. In losse figuren is dit geen punt, maar als je de krachten in één complete figuur tekent, dan zegt de pijlpunt niets meer. Het teken (+ voor trek en - voor druk) blijft wel relevant.

Op de kop van F₁ zet ik de andere bekende kracht, de ondersteuningskracht F_q (andersom had ook gemogen). Teken op de kop van F_q weer een werklijn in de richting van één van de twee onbekende krachten (hier: kracht in staaf 3, blauw) en op de staart van F₁ een werklijn in de richting van de andere onbekende kracht (hier: kracht in staaf 4, zwart). De werklijnen snijden elkaar weer, samen met de bekende krachten vormen deze een gesloten krachtenveelhoek. Bedenk dat de pijlen kop-op-staart staan, hieruit valt af te leiden dat F₃ een drukkracht is en F₄ een trekkracht. De lengtes van de pijlen representeren de grootte van de krachten.

Zo kan je door naar knooppunt C: F₂ en F₃ zijn bekend, er zijn maar twee onbekende krachten over, dus met eenzelfde constructie zijn deze te bepalen.

Hopelijk kan je hiermee verder.

zondag 20 mei 2018

©2001-2024 WisFaq