Extreme waarden bij afgeleide van wortelfunctie

Hi,

Ik moet de extreme waarden van deze functie berekenen:
$f(x)=x-2\sqrt{x-1}$

De afgeleide functie is:
$\eqalign{f'(x)=1-\frac{1}{\sqrt{x-1}}}$

Ik kom er alleen niet uit, kun je me hierbij helpen?

Alvast bedankt

Mariam
Leerling bovenbouw havo-vwo - zaterdag 12 mei 2018

Antwoord

Voor het berekenen van de extremen bepaal je de afgeleide. Je stelt de afgeleide gelijk aan nul en lost de vergelijking op. Dat geeft je mogelijke kandidaten voor de extremen van je functie:



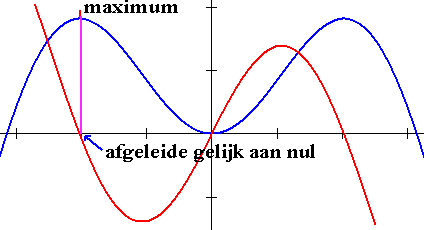
De rode grafiek is de afgeleide van de blauwe grafiek. Je kunt zien dat de afgeleide gelijk aan nul is bij de toppen. De afgeleide is nul betekent dat de richtingscoëfficiënt van de raaklijn nul is en dat betekent dat de raaklijn horizontaal loopt. Bij de extremen is de afgeleide gelijk aan nul.

In dit geval wordt dat:

$
\eqalign{
& 1 - \frac{1}
{{\sqrt {x - 1} }} = 0 \cr
& \frac{1}
{{\sqrt {x - 1} }} = 1 \cr
& \sqrt {x - 1} = 1 \cr
& x - 1 = 1 \cr
& x = 2 \cr}
$

Maak een schets/plot van de grafiek van $f$ en trek je conclusies.



Bij $x=2$ heb je kennelijk te maken met een minimum. Het minumum is $f(2)=0$.

• Differentiëren
• Re: Wat heb je aan de afgeleide?
• 5. Zoeken naar maxima en minima

zondag 13 mei 2018

Re: Extreme waarden bij afgeleide van wortelfunctie

©2001-2024 WisFaq