Toepassen differentiaalvergelijking

Hallo,

Ik ben bezig met een opgave waar je m.b.v. een differentiaalvergelijking de oplossing moet kunnen vinden. Maar ik loop vast halverwege. Ik heb plaatjes ingestuurd voor het gemak.

Op het ruitjespapier heb ik geprobeerd de vraag te beantwoorden.

De onderste regel geeft de uiteindelijke formule waaruit 2mg/liter en 38.4 uur moet komen.

Lizzy
Student universiteit - maandag 30 april 2018

Antwoord

Hallo Lizzy,

Tot en met het opstellen van de integraal gaat het wel goed, maar daarna maak je er een rommeltje van. Ten eerste: na primitiveren hoort 'dm' niet meer in je vergelijking voor te komen. Verder: t/5 is niet hetzelfde als t^-5. In je e-macht is de variabele 'm' verdwenen, en je hebt een rekenfout gemaakt: 0,3/5=0,06 en niet 0,6.
Noteer zorgvuldig, dat voorkomt dit soort vergissingen, en neem niet te grote denkstappen.

Hieronder zie je mijn uitwerking:



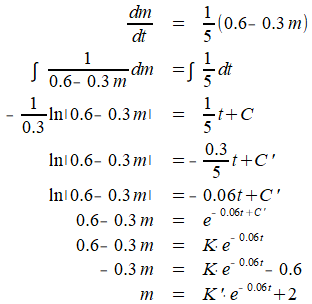
Voor t=0 geldt: m=0. Wanneer je deze randvoorwaarde in de laatste vergelijking invult, vind je: K'=-2. Hiermee wordt de uiteindelijke oplossing:

m = -2e^-0,06t+2.

Voor zeer grote waarden van t gaat de e-macht naar nul, zodat m uiteindelijk naar 2 mg/liter gaat.
Dit hadden we ook vooraf kunnen inzien: wanneer de concentratie een eindwaarde bereikt, is de verandering dm/dt=0. In de op te lossen vergelijking zien we dan:

0,6-0,3m = 0

Ook hieruit volgt: m=2 mg/liter.

Nu je de juiste formule hebt, kan je de overige vragen wel beantwoorden, denk ik. Voor een algemene waarde van $\alpha$ volg je precies dezelfde procedure. De in te stellen waarde van $\alpha$ om m=0,5 te bereiken, kunnen we op dezelfde manier voorspellen:
Uiteindelijk moet gelden:

dm/dt=0

dus:

$\alpha$-0,3m=0

Voor m=0,5 wordt dit:

$\alpha$=0,3·0,5
$\alpha$=0,15.

Maar dit moet natuurlijk ook uit jouw oplossing van de differentiaalvergelijking komen!

maandag 30 april 2018

©2001-2024 WisFaq