Re: Loodrecht snijden
Ja, ik kwam al niet uit om de vergelijking $f(x)=g(x)$ op te lossen*. Maar ik wist niet dat je het punt $A(3,0)$ mocht gebruiken. Als vraag $a.$ niet gesteld zou zijn, dan zou je het toch via uw manier gedaan moeten hebben? In plaats van ervan uit gaan dat het snijpunt A blijft?
De vervolgvraag gaat over de oppervlakte berekenen tussen de grafiek $f(x)$, $g(x)$ en de $y$-as. Waarbij V=4√3 (ik heb nu foto van de vraag in de mail gestuurd, misschien helpt dat ;))
Mvg,
Anna
Anna
Leerling bovenbouw havo-vwo - zaterdag 14 april 2018
Antwoord
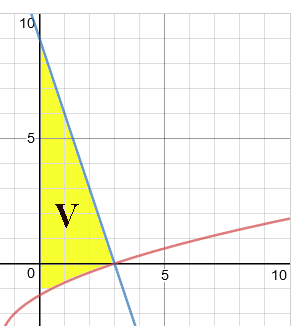
De oppervlakte van V moet gelijk zijn aan $
4\sqrt 3
$. Voor dat vlakdeel V geldt:
$
\eqalign{
& \int\limits_{x = 0}^3 {p(x - 3) - \left( { - 3 + \sqrt {2x + 3} } \right)\,\,dx} = 4\sqrt 3 \cr
& \int\limits_{x = 0}^3 {p(x - 3) + 3 - \sqrt {2x + 3} \,\,dx} = 4\sqrt 3 \cr
& ... \cr}
$
Ga na dat dat klopt!
...de rest volgt dan (bijna) vanzelf...
Maar dan moet je dan even zelf proberen!- Er is nog een oplossing! Enig idee?
Mocht het niet lukken dan horen we 't wel...
PS
Weet je al wat er uit komt?
Ik had $
\eqalign{p = - \frac{2}
{3}\sqrt 3}
$ en nog een oplossing...
Klopt dat?
NASCHRIFT
$
\eqalign{
& \int\limits_{x = 0}^3 {p(x - 3) - \left( { - 3 + \sqrt {2x + 3} } \right)\,\,dx} = 4\sqrt 3 \cr
& \int\limits_{x = 0}^3 {p(x - 3) + 3 - \sqrt {2x + 3} \,\,dx} = 4\sqrt 3 \cr
& \left[ {\frac{1}
{2}px^2 - 3px + 3x - \frac{1}
{3}\sqrt {\left( {2x + 3} \right)^3 } } \right]_{x = 0}^{x = 3} = 4\sqrt 3 \cr
& \frac{1}
{2}p \cdot 3^2 - 3p \cdot 3 + 3 \cdot 3 - \frac{1}
{3}\sqrt {\left( {2 \cdot 3 + 3} \right)^3 } - ... \cr
& \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,...\left( {\frac{1}
{2}p \cdot 0^2 - 3p \cdot 0 + 3 \cdot 0 - \frac{1}
{3}\sqrt {\left( {2 \cdot 0 + 3} \right)^3 } } \right) = 4\sqrt 3 \cr
& 4\frac{1}
{2}p - 9p + 9 - 9 + \sqrt 3 = 4\sqrt 3 \cr
& - 4\frac{1}
{2}p - = 3\sqrt 3 \cr
& - 9p = 6\sqrt 3 \cr
& p = - \frac{2}
{3}\sqrt 3 \cr}
$
*Zie...
zaterdag 14 april 2018
©2001-2024 WisFaq
|
Dit is een reactie op vraag 86096