Zesëntwintig bollen met letters

In een doos zitten 26 bollen, elk met een andere letter van het alfabet. Piet haalt er één voor één zeven uit, noteert de letter en werpt de bol terug in de doos. Hoe groot is de kans dat hij met de genoteerde letters zijn naam kan vormen ?

Mijn oplossing :

Stel X is de gebeurtenis dat {P,I,E,T} wordt getrokken
Stel nX is het complement van X (nX = S/X met S = X U nX)

P(X) = 1 - P(nX)
F(X) = 26⁷ - F(nX)
waarbij F verwijst naar de aantal mogelijke uitkomsten en
26⁷ = 26 tot de 7de macht voorstelt

Stel A is de gebeurtenis dat de letter P niet wordt getrokken
Stel B is de gebeurtenis dat de letter I niet wordt getrokken
Stel C is de gebeurtenis dat de letter E niet wordt getrokken
Stel D is de gebeurtenis dat de letter T niet wordt getrokken

$\Rightarrow$ nX = A U B U C U D
$\Rightarrow$ P(nX) = P(A U B U C U D)
$\Rightarrow$ P(nX) = P(A) + P(B) + P(C) + P(D)
- P(AB) - P(AC) - P(AD) - P(BC) - P(BD) - P(CD)
+ P(ABC) + P(ABD) + P(ACD) + P(BCD)
- P(ABCD)

Hierbij noteer ik gemakshalve AB voor A doorsnede B, AC voor A doorsnede C, ... , ABCD voor A doorsnede B doorsnede C doorsnede D.

Er geldt nu F(A) = F(B) = F(C) = F(D) = 25⁷
F(AB)= F(AC) = F(AD) = F(BC) = F(BD) = F(CD) = 24⁷
F(ABC) = F(ABD) = F(ACD) = F(BCD) = 23⁷
F(ABCD) = 22⁷
$\Rightarrow$ F(nX) = (4 x 25⁷) - (6 x 24⁷) + (4 x 23⁷) - 22⁷
$\Rightarrow$ F(nX) = 8.020.177.856
$\Rightarrow$ F(X) = 26⁷ - F(nX)
$\Rightarrow$ F(X) = 8.031.810.176 - 8.020.177.856 = 11.632.320
$\Rightarrow$ P(X) = F(X)/26⁷ = 11.632.320/8.031.810.176
$\Rightarrow$ P(X) = 0,001448281 ~= 0,0014

Vreemd genoeg geeft het boek als uitkomst 0,0013
Heb ik iets over het hoofd gezien ? Of geeft het boek een foute uitkomst ?

Rudi
Ouder - woensdag 11 april 2018

Antwoord

De methode ziet er goed uit. Het enige dat ik kan bedenken is dat het boek met afgeronde waarden heeft gewerkt van de individuele kansen.

Hier is een screenshot met daarin twee manieren om die kansen bij elkaar op te tellen, en elk met twee afrondingen: 10 cijfers, of 5 cijfers.


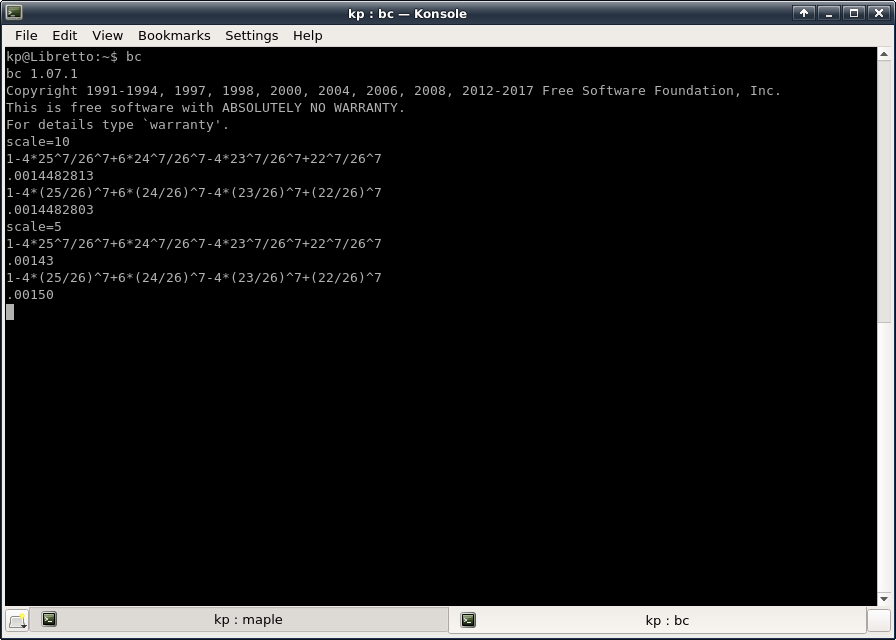
Klik afbeelding voor een vergroting
Je ziet dat zelfs $(25/26)^7$ versus $25^7/26^7$ nemen al verschil kan maken.

In Maple kreeg ik na exacte berekening jouw antwoord ook.

kphart
donderdag 12 april 2018

Re: Zesëntwintig bollen met letters

©2001-2024 WisFaq