Resultante berekenen en hoek tussen resultante en vector

Bij een oefening komt voor dat er tussen F1 (verticaal, 100N) en F2 (100 N) een hoek is van 60°. tussen F1 en F3 (200N) is er een hoek van -60°.

Nu moeten we de resultante berekenen en de grootte van hoek die deze vormt met F3.

Ik begin dus met de resultante te zoeken tussen F1 en F2, dan kom ik alweer een niet afgerond getal uit. En dan zou ik met die resultante en F3 een andere resultante moeten bekomen. Maar ik kom er maar niet bij.

Hoe begin ik er dan aan? en hoe zoek ik dan de ingesloten hoek die je gebruikt in de formule om je resultante te vinden?

Admin
Iets anders - zaterdag 10 maart 2018

Antwoord

Voor de beantwoording maken we eerst een schets:



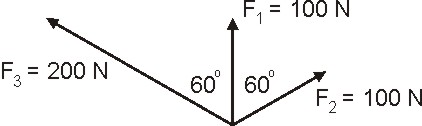
We kiezen een assenstelsel: naar rechts is positief (x), naar boven is positief (y). Dan ontbinden we de gegeven krachten in x- en y-richting:

F_1,x = 0
F_2,x = 100·sin(60°) = 50√3 N
F_3,x = -200·sin(60°) = -100√3 N

Opgeteld levert dit de x-component van de resulterende kracht:

F_res,x = -50√3 N -86,6 N (dus 86,6 N naar links).

Hetzelfde voor de y-richting:

F_1,y = 100 N
F_2,y = 100·cos(60°) = 50 N
F_3,y = 200·cos(60°) = 100 N

F_res,y = 250 N naar boven.

Onderstaande figuur geeft dit resultaat weer:



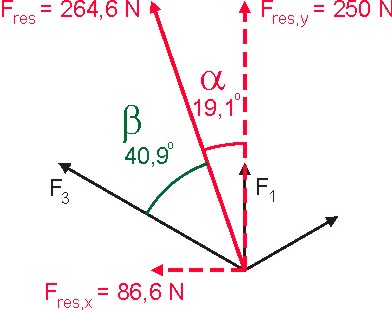
De grootte van de resulterende kracht vinden we met behulp van Pythagoras:

(F_res)² = (F_res,x)²+(F_res,y)²

(F_res)² = (-50√3)²+250² = 70000
F_res = √70000 264,6 N

Dan nog de richting van deze resulterende kracht. In de figuur is te zien dat voor de hoek $\alpha$ tussen F_res en de verticaal geldt:

Tan($\alpha$) = ^F_res,x/_Fres,y
Tan($\alpha$) = ^86,6/₂₅₀
$\alpha$ = tan^-1(^86,6/₂₅₀)
$\alpha$ 19,1°

Voor de hoek $\beta$ tussen F_res en F₃ blijft dan over:

$\beta$ = 60-19,1 = 40,9°

zaterdag 10 maart 2018

©2001-2024 WisFaq