Vectoren en zwaartepunten

Hallo,

Ik heb een probleempje met de theorie over het zwaartepunt bepalen door middel van vectoren. De bedoeling bij dit plaatje (die ik als bijlage heb toegevoegd) is het verklaren dat de formule voor vector z = vector a + 3/7(vector b - vector a).

Ik snap ten eerste niet waarom het vector b - vector a is om vector z te krijgen, want vector a lijkt langer dan vector b dus dan komt iets negatiefs uit, het lijkt voor mijn gevoel eerder op vector a + vector b? En ten tweede waarom hebben ze 3/7 genomen en niet 4/7? Ik hoop dat iemand mij hierbij kan helpen. Alvast bedankt!

Mvg,
Anna

Anna
Leerling bovenbouw havo-vwo - vrijdag 2 maart 2018

Antwoord

Hallo Anna,

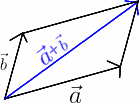
Waarschijnlijk weet je dat er (grafisch) twee methoden zijn om de som van twee vectoren te vinden (zie ook Wikipedia: vector). Eén methode is via een parallellogram:



Voor jouw vraag is een tweede methode handiger, de 'kop-staart-methode'. Om de som van vector a en vector b te vinden, plaats je de 'staart' van vector b op de 'kop' van vector a. De somvector loopt dan vanaf de staart van de eerste vector naar de kop van de tweede vector:



Nu jouw vraag: vector b - vector a is een vector in de richting van A naar B, en met de lengte AB. Om vector z te vinden, nemen we eerst vector a, en met de 'kop-staart-methode' moet hier een vecor bij opgeteld worden die loopt van A naar Z. Dit is in de richting van vector b - vector a, maar de lengte is slechts 3/7 van de totale afstand van A naar B. Vandaar:

vector z = vector a + 3/7(vector b - vector a)



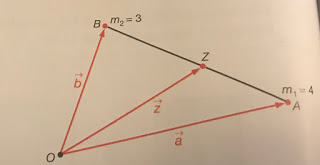
We kunnen ook eerst naar B 'reizen' en vervolgens 4/7 van de afstand BA afleggen (dus in omgekeerde richting, ofwel in de richting vector a - vector b). Dan krijgen we:

vector z = vector b + 4/7(vector a - vector b)

Als je de haakjes wegwerkt, zal je zien dat je in beide gevallen krijgt:

vector z = 4/7·vector a + 3/7·vector b.

vrijdag 2 maart 2018

©2001-2024 WisFaq