Re: Van CDF naar PDF
Waarom niet? Bij het invullen van x=1 en x=2 komt er respectievelijk F(x)=0 en F(x)=1 uit. Waarom is dit niet te differentiëren en x=1.5 bijvoorbeeld wel (met F(1.5)=1/3
Walter
Student universiteit - donderdag 23 november 2017
Antwoord
Bekijk de definitie van differentieerbaarheid en de afgeleide nog maar eens: voor differentieerbaarheid in $2$, bijvoorbeeld, moet de limiet
$$
\lim_{x\to2}\frac{F(x)-F(2)}{x-2}
$$
bestaan (en die bestaat niet).
Hieronder de grafiek van $F$ op het interval $[1,2]$; het lijkt of $F$ toch wel differentieerbaar is in $1$.
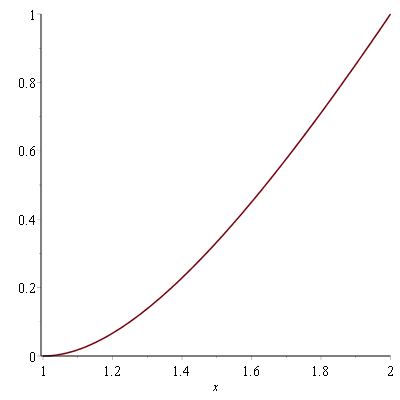
Bepaal de limiet
$$
\lim_{x\to1}\frac{F(x)-F(1)}{x-1}
$$
maar eens.
kphart
donderdag 23 november 2017
©2001-2024 WisFaq
|
Dit is een reactie op vraag 85242