Pythagoras

Als je bijvoorbeeld driehoek BDE hebt en je hebt 2 zijden maar wil de andere ook weten welke formule moet je dan opstellen om die lijn uit te reken en hoe kom je daar achter?

Anne
Leerling bovenbouw havo-vwo - zondag 15 oktober 2017

Antwoord

Hallo Anne,

Wanneer het over rechthoekige driehoeken gaat, gebruik je de stelling van Pythagoras. Voor een driehoek met zijden a, b en c weet je waarschijnlijk dat deze luidt:



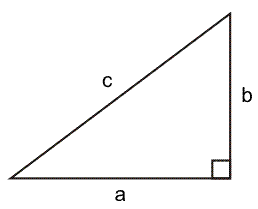
a²+b²=c²

Je moet wel goed opletten op welke plaats je de lengtes in de formule invult:

• De kwadraten die je bij elkaar optelt, gaan altijd over de rechthoekszijden.
  
• Het kwadraat dat 'apart' staat, gaat altijd over de schuine zijde

Wanneer twee rechthoekszijden gegeven zijn, bereken je de onbekende schuine zijde als volgt:

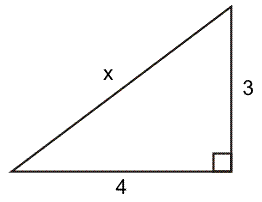
• Formule opschrijven zoals je deze hebt geleerd:
  a²+b²=c²
  
• De bekende waarden op de juiste plaats invullen:
  4²+3²=x²
  
• Berekening verder uitwerken:
  16+9=x²
  x²=25
  x=5

Wanneer een rechthoekszijde en een schuine zijde gegeven zijn, dan vul je de formule op een iets andere manier in:

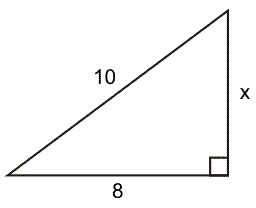
• Formule opschrijven zoals je deze hebt geleerd:
  a²+b²=c²
  
• De bekende waarden op de juiste plaats invullen:
  8²+x²=10²
  (Heb je gezien dat de onbekende x² nu niet apart staat maar bij 8² wordt opgeteld?)
  
• Berekening verder uitwerken:
  64+x²=100
  x²=100-64
  x²=36
  x=6

Je ziet: wanneer je er goed op let dat je de onbekende lengte op de juiste plaats invult, dan volgt de juiste berekening vanzelf.

Sommige leerlingen vinden het prettig om een rekenschema te gebruiken. Uitleg hierover vind je bij De stelling van Pythagoras.

Omdat je in de titel 'Pythagoras' noemt, ga ik er even van uit dat jouw vraag alleen over rechthoekige driehoeken gaat. Voor niet-rechthoekige driehoeken gebruik je de cosinusregel. Mocht je hierover vragen hebben, laat dit dan gerust weten.

zondag 15 oktober 2017

©2001-2024 WisFaq