Hoeken in een figuur berekenen

Ik moet mbv het inproduct de hoeken berekenen van een figuur.
Bv van de vierhoek met A(0,3) B(-2,-1) C(3,1) en D(5,5)
Ik zoek richtingsgetallen van de rechten, en bepaal de hoek, maar hoe kan ik weten dat het soms de scherpe hoek en soms de stompe hoek is?

Vannes
3de graad ASO - woensdag 24 mei 2017

Antwoord

Laat ik als voorbeeld hoek A en hoek B berekenen.

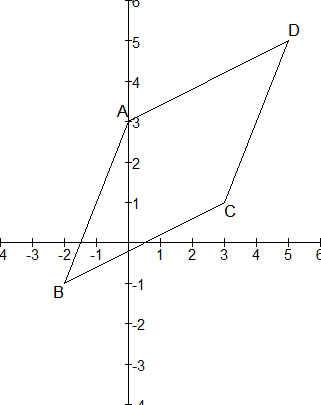
Hoek A:
De vector AD=(5-0,5-3)=(5,2)
De vector AB=(-2-0,-1-3)=(-2,-4)
Voor de cosinus van de hoek tussen de vectoren AD en AB vinden we dan:
(5,2)·(-2,-4)/(√29·√20)=(-10-8)(√29·√20)=-18/(√29·√20)
Aan het feit dat het inproduct negatief is kun je zien dat hoek A stomp is.

Nu hoek B:
De vector BA=(0--2,3--1)=(2,4)
De vector BC=(3--2,1--1)=(5,2)
Het inproduct van de vectoren BA and BC is (2,4)·(5,2)=10+8=18
Dit inproduct is positief, hoek B is dus scherp.

woensdag 24 mei 2017

©2001-2024 WisFaq