
Er zijn twee driehoeken ABC. Welke?
Gegeven is dat er twee driehoeken ABC zijn met AB = 20, AC = 13 en $\angle$B = 33°. Blijkbaar kan er aan deze voorwaarden worden voldaan met twee verschillende waarden van BC. De eerste BC heb ik berekend met de cosinusregel, hoe vind ik de andere? Eerst dacht ik aan de stelling van Stewart, maar dan zou het geen twee maal ABC zijn...
Mario
Leerling bovenbouw havo-vwo - zaterdag 13 mei 2017
Antwoord
Eerst maar 's een tekening!
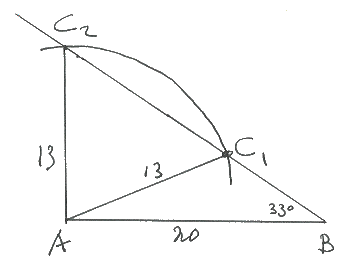
Met de cosinusregel?
Invullen van $
b^2 = a^2 + b^2 - 2ab\cos \beta
$ geeft:
$
13^2 = a^2 + 20^2 - 2 \cdot a \cdot 20 \cdot \cos 33^\circ
$
Met je GR oplossen geeft:
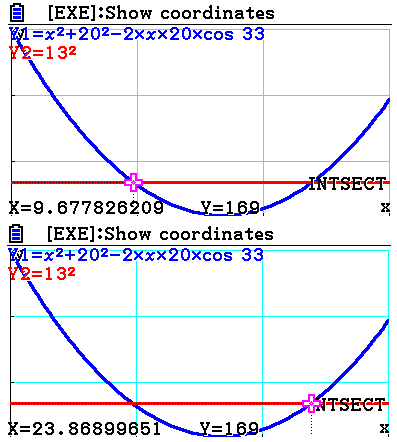
$
a \approx {\text{9}}{\text{,68}} \vee a \approx {\text{23}}{\text{,87}}
$
Maar er zijn natuurlijk meer wegen die naar Rome leiden, maar zo kan het. Hopelijk helpt dat?

zaterdag 13 mei 2017
 ©2001-2024 WisFaq
©2001-2024 WisFaq
|