Re: Afstand in een trapezium
Bedankt voor je reactie.
Nu weet ik alleen niet hoe ik verder kom om MN te bereken. Omdat |NP| niet precies 0,5 is.
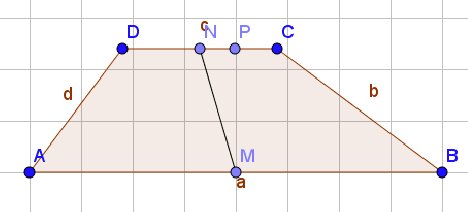
Plaatje later toegevoegd
Gonnek
Student hbo - woensdag 1 maart 2017
Antwoord
Wat is $P$? Die is nog niet ter sprake geweest. Maar je kunt nu $D$ loodrecht op $AB$ projecteren en daarmee uitrekenen waar de loodrechte projectie van $N$ op $AB$ ligt. Dan moet het lukken.
Naschrift: ik heb nu het plaatje gezien; daar was in de vraag niets over gezegd.
Ik neem aan dat $P$ de loodrechte projectie van $M$ op $CD$ is. In dat geval kun je $NP$ vinden door eerst $C$ op $AB$ te projecteren, zeg op het punt $Q$. Dan is $CQB$ ook een $3$-$4$-$5$-driehoek, dus weet je de afstand $BQ$ en dus ook $QM$, en daarmee ook $CP$ en $PN$.
kphart
woensdag 1 maart 2017
©2001-2024 WisFaq
|
Dit is een reactie op vraag 83938