Onder één noemer brengen

De opbrengst O en de kosten K van een zeker artikel zijn gegeven door de functies O(q)=(4q+500) en K(q)=1/20q
De winst W wordt bepaald door W=O-K. Gevraagd wordt O'(q) te bereken en te bewijzen dat
W'(q)=40-(4q+500)/20(4q+500).
Ik heb O'(q) berekend met de kettingregel als volgt:
O(q)=(4q+500)
p(h)=h en h(q)=4q+500
O'(g)= p'(h) x h'(q)
= 1/2h x 4
= 4/2h
= 4/2(4q+500)
= 2/(4q+500)
Ik heb dus O'(q) berekend, K'(q)= 1x1/20= 1/20
Ik kan bij W'(q) de somregel gebruiken dus
2/(4q+500) - 1/20. Alleen vanaf hier zit ik vast, ik zie niet hoe ik op
W'(q)= 40-(4q+500)/20(4q+500) kan uitkomen.
Kunt u mij helpen?

wouter
Iets anders - zondag 2 maart 2003

Antwoord

Als ik goed zie gaat het alleen om deze laatste stap:



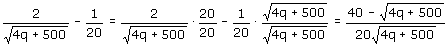
Dit noemen we wel 'onder één noemer brengen'.

Zie Wat is onder één noemer brengen?

zondag 2 maart 2003

©2001-2024 WisFaq