Minimale oppervlakte cilinder bij gegeven inhoud

Je hebt een cilinder van 0,1 dm³ en je moet berekenen wat je voor de straal moet invullen om een zo klein mogelijk opp. te krijgen.

BB
Leerling bovenbouw havo-vwo - donderdag 27 februari 2003

Antwoord

Je hebt twee formules:

1. Oppervlakte=2pR²+2pR·h (1)

   Hierbij is de eerste term de oppervlakte van grond- en bovencirkel en de tweede term de oppervlakte van de cilindermantel.

2. Inhoud=pR²·h

   Hierbij is pR² de oppervlakte is van het grondvlak en h de hoogte.

Ik weet: inhoud=0,1 dm³. Hiermee kan je h uitdrukken in R. Namelijk:
h=0,1/(pR²)

Als je deze laatste uitdrukking invult in (1) krijg je:
Oppervlakte=2pR²+2pR·0,1/(pR²)
Oppervlakte=2pR²+0,2/R

Hiermee hebben we de oppervlakte uitgedrukt in R. Voor welke waarde van R is de oppervlakte het kleinst?
Voer deze functie in je rekenmachine in:
y1=2´p´x²+0.2/x
En lees/bepaal het minimum en je bent er uit.

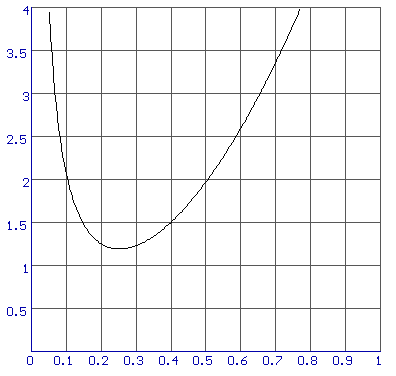
Zie vraag 170

donderdag 27 februari 2003

©2001-2024 WisFaq