Cyclometrische functies

Hallo!
Kunt u me vertellen hoe ik deze oefening moet aanpakken?
cos($\pi$/2+Bgcos(2/3)) = ?

Alvast bedankt!!

Prince
3de graad ASO - zondag 17 april 2016

Antwoord

Bedenk dat Bgcos(²/₃) de hoek is waarvan de cosinus gelijk is aan ²/₃. In onderstaande figuur heb ik een rechthoekige groene driehoek getekend met schuine zijde 1 en horizontale zijde ²/₃. De cosinus van de hoek links is dan precies deze hoek, ik noem die hoek $\alpha$:



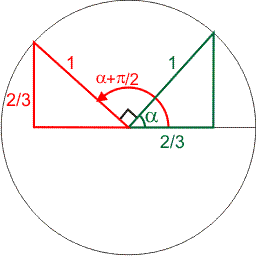
Vervolgens tel ik $\pi$/2 radialen op, daarbij kan ik de rode driehoek tekenen. De schuine zijde is nog steeds 1, nu is de verticale zijde gelijk aan ²/₃. De horizontale zijde geeft de gevraagde cosinus van deze hoek weer. Deze horizontale zijde kan je met Pythagoras berekenen. Maar let op: vergeet het min-teken niet, want deze zijde 'wijst naar links'.

zondag 17 april 2016

©2001-2024 WisFaq