Oppervlakte kegelmantel en grondcirkel

Beste mevrouw, meneer,

Kunt u mij aub deze som uitleggen, want ik snap niet hoe ik het moet aanpakken.
Er zit een plaatje bij die ik naar jullie heb gestuurd.
Het gaat om vraag B t/m F
b. Hoe gro0t is de omtrek van de grondcirkel?
c. Bereken de straal van de grondcirkel
d. De kegel wordt verticaal middendoor gesneden. Teken de doorsnede op ware grootte.
e. Bereken in de doorsnede de hoogte van de kegel in twee decimalen
f. Bereken de inhoud van de kegel in 2 decimalen.

Ik hoop dat u mij kunt helpen deze som te begrijpen.

Met vriendelijke groet,
Marian

Marian
Leerling onderbouw vmbo-havo-vwo - woensdag 6 april 2016

Antwoord

Hallo Mirian,

Het plaatje dat je stuurde laat zien hoe je van een halve cirkel een kegelmantel kunt maken:



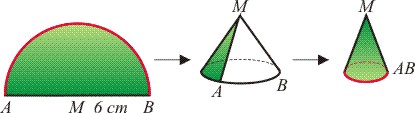
De punten A en B leg je op elkaar, het punt M komt dan omhoog en wordt de top van de kegel. Wanneer dit niet duidelijk is, knip dan maar eens een halve cirkel uit een stuk stevig papier en maak hiervan een 'feesthoedje'.

De rode boog (halve cirkel) wordt uiteindelijk de omtrek van de grondcirkel van de kegel. Hiermee is vraag b te beantwoorden:

• Bereken de lengte van de rode boog (= halve omtrek van een cirkel)
  
• De omtrek van de grondcirkel is net zo lang, je weet dus de omtrek van de grondcirkel

Vraag c kan je nu ook vast wel beantwoorden: je weet de omtrek van de grondcirkel. Met de formule voor de omtrek van een cirkel kan je de straal uitrekenen.

De doorsnede van de kegel is een gelijkzijdige driehoek. De basis is de diameter van de grondcirkel, de lengte van de schuin omhoog lopende zijden is gelijk aan AM in je linker figuur.

Met behulp van Pythagoras kan je nu de hoogte van de kegel uitrekenen. En met deze hoogte kan je weer de inhoud berekenen.

Lukt het hiermee? Laat maar weten wanneer je ergens vastloopt.

donderdag 7 april 2016

©2001-2024 WisFaq