Thales

Als 2 evenwijdige rechten m en n drie willekeurige door 1 punt P gaande rechten a,b en c snijden, in A,B en C,D en E,F respectievelijk, ik vroeg mij af of dan geldt:
AC:BD=PC:PD en CE:DF=PC:PD en zo ja waarom maw is dit te bewijzen?
Volgens Thales geldt: PA:PB=PE:PF.
Ik vraag me ook af of geldt:PA:PB=PC:PD en zo ja waarom maw is dat ook te bewijzen?

Geldt bovenstaande ook als P tussen m en n ligt.
Misschien is het handig als u met uw welnemen ter verduidelijking een figuur maakt.

Voor de duidelijkheid dus:
A,C en E liggen op de rechte m.
B,D en F liggen op de rechte n.

Herman
Ouder - vrijdag 22 januari 2016

Antwoord

We bekijken eerst deze figuur:



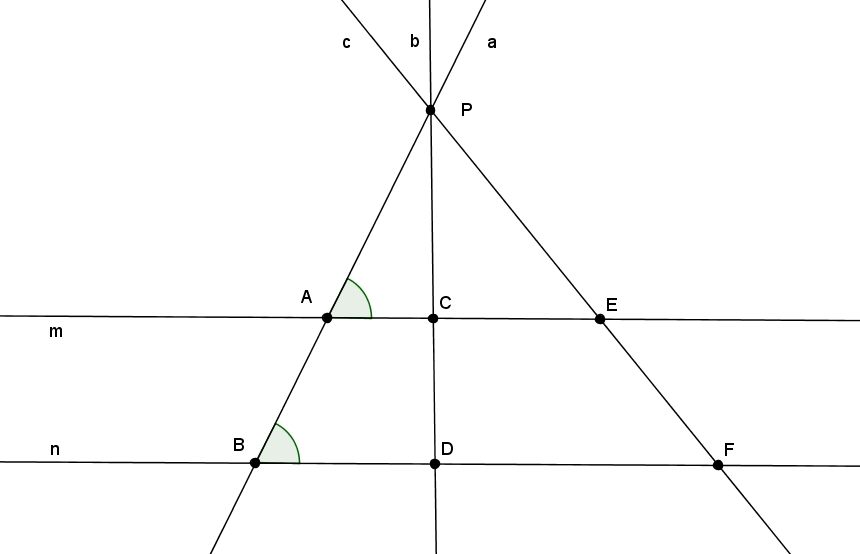
In deze figuur zien we dat de gemarkeerde hoeken bij A en B F-hoeken zijn.

• Dat betekent dat $\Delta PAC$ en $\Delta PBD$ twee gelijke hoeken hebben. Daarmee zijn ze gelijkvormig. Om die reden geldt $PA : PB = PC : PD = AC : BD$
  
• Dat betekent ook dat $\Delta PAE$ en $\Delta PBF$ twee gelijke hoeken hebben. Daarmee zijn ook deze gelijkvormig. En dus geldt ook $PA : PB = PE : PF = AE : BF$
  
• Op vergelijkbare wijze kun je ook zien dat $\Delta PCE$ en $\Delta PDF$ twee gelijke hoeken hebben en gelijkvormig zijn. Dus geldt ook $PC : PD = PE : PF = CE : DF$
  

Combineren van deze gelijke verhoudingen beantwoordt al je vragen bevestigend als P niet tussen m en n ligt. Wat verandert er als dat wel zo is?



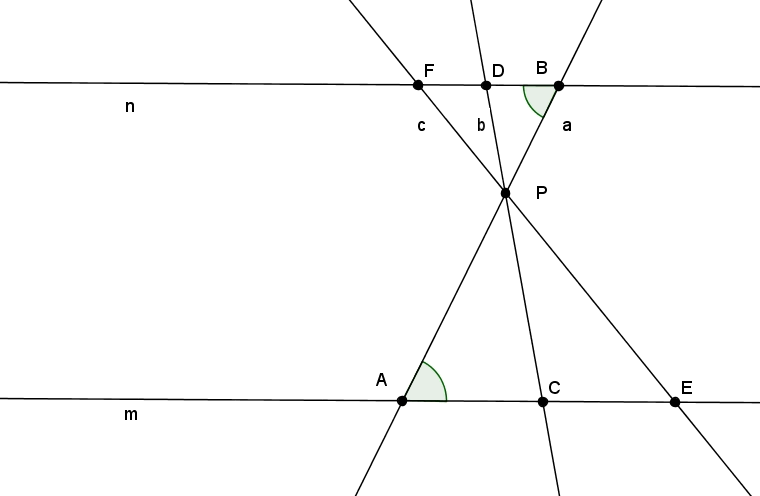
Twee dingen. De gemarkeerde hoeken zijn nu geen F-hoeken, maar Z-hoeken. En de twee hoeken $\angle APC$ en $\angle BPD$ zijn niet meer dezelfde hoek, maar overstaande hoeken - dus wel gelijk. Je kunt dus verder bovenstaande redeneringen opnieuw toepassen.

Met vriendelijke groet,

zaterdag 23 januari 2016

©2001-2024 WisFaq