Logaritmische functie roteren

Goedemiddag
We zijn bezig met logaritmische functies. We kregen deze oefening:
De grafiek, G, van y=logx wordt over een hoek van 90° rond de oorsprong geroteerd in tegenwijzerzin. Zo bekomt men een nieuwe grafiek G'. Welke van de volgende vergelijkingen is een grafiek voor G'?

a) y=log((x+90)/9)
b) y=de x-logaritme van 10
c) y=1/(x+1)
d) y=10^-x
e) y=10^x

We mogen niet zomaar de grafieken tekenen en daaruit het antwoord afleiden maar we moeten het berekenen of toch de stappen opschrijven. Ik weet niet hoe ik dat moet doen.
Met vriendelijke groeten
Sarah

Sarah
3de graad ASO - zaterdag 14 november 2015

Antwoord

Hallo Sarah,

Hieronder heb ik in een assenkruis een willekeurig punt P van de grafiek van G getekend (links). De groene pijl geeft de x-coördinaat weer, de rode pijl de y-coördinaat.



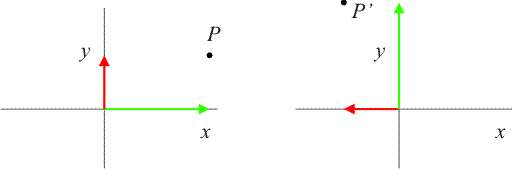
Rechts is de grafiek 90° geroteerd. Je ziet:

• De oude x-coördinaat (groen) is nu de nieuwe y-coördinaat;
  
• De oude y-coördinaat (rood) is nu het tegengetelde van de nieuwe x-coördinaat.

Voor je nieuwe functie betekent dit:

x wordt y;
y wordt -x:

y=log(x) wordt -x=log(y)

Nu moet je dit voorschrift natuurlijk nog even netjes omschrijven zodat het de vorm krijgt:

y=.....

Lukt het hiermee?

zaterdag 14 november 2015

©2001-2024 WisFaq