Ln met breuk

Heb volgende week een tentamen en snap deze sommen totaal niet...
HOpelijk kunnen jullie mij hierbij helpen..

afgeleide van ln(-2x+8/-9x+2)
afgeleide van ln²(4x+6)
afgeleide van 7⁷-7x
2e afgeleide van (8x+1)7³x⁸ $\to$ het antwoord is: 384 7³ x⁷ ln(7) +576(8x+1)7³x⁸ x¹⁴ln(7)+168(8x+1)7³x⁸ x⁶ ln(7)
2e afgeleide van x²/x+1

Een vraagje buiten deze sommen; is e³³ gewoon 1?

Alvast hartstikke bedankt, jullie site is geweldig!

Studen
Student universiteit - woensdag 16 september 2015

Antwoord

Beste Nina,

Dit zijn wel veel vragen in één keer. Ik zal enkele vragen uitwerken en wat uitleg geven. Op dezelfde wijze kan je de overige vragen aanpakken.

Opgave 1:


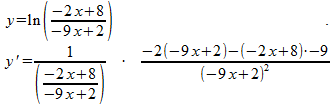
Het deel links van de vermenigvuldigingspunt is toepassing van de regel:

y=ln(x) geeft: y'=1/x

Rechts van de vermenigvuldigingspunt is toepassing van de kettingregel: achter de ln-functie staat niet 'zomaar' x, maar een quotiëntfunctie van x. Je moet dus nog vermenigvuldigen met de afgeleide van dit quotiënt, hiervoor gebruik je de quotiëntregel.
Hierna is het een kwestie van vereenvoudigen:



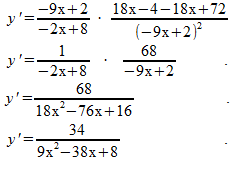
Opgave 2:


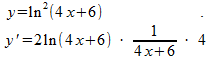
Links van de vermenigvuldigingspunt is toepassing van de regel:

y=x² geeft: y'=2x

Dan komt de kettingregel: je moet vermenigvuldigen met de afgeleide van de ln-functie. De afgeleide van ln(x) is 1/x.
Maar: de ln-functie 'werkt' niet op x, maar op (4x+6). Je moet dus nogmaals de kettingregel toepassen: vermenigvuldigen met de afgeleide van (4x+6), dus met 4.

Dan is het weer een kwestie van vereenvoudigen:



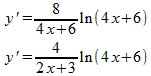
Opgave 3:


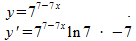
Links van de vermenigvuldigingspunt is toepassing van de regel:

y=a^x geeft: y'=a^xln(a)

Dan komt weer de kettingregel: in de exponent staat niet 'zomaar' x, maar een functie van x: 7-7x. Je moet dus vermenigvuldigen met de afgeleide hiervan, dus met -7.
Ook nu is de rest een zaak van vereenvoudigen:



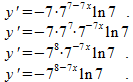
Pak de overige vragen op dezelfde manier aan. Het is vooral consequent werken, voldoende tussenstappen noteren om vergissingen te voorkomen.

Wat betreft jouw laatste vraag: e³³ is zeker niet gelijk aan 1. Volgens mijn rekenmachine is dit ongeveer 2,146·10¹⁴!

donderdag 17 september 2015

Re: Ln met breuk

©2001-2024 WisFaq