Vector vergelijking

Beste wisfaq,
Krachtengrootte en hoeken in graden vanuit een punt P in een vlak:
16(a gr)+25(b gr.)+10(0 gr)-14(30 gr.)+30(160 gr.)= 0
gevr.grootte van a en b
De resultante van de bekenden is een kracht 30,48.

De hor.comp. en de vert. comp, van de onbekenden:

16cos(a)+25cos(b) resp. 16sin(a)+25sin(b)

na kwadratering en optellen = 30,48^2
Dit geeft cos(a)cos(b)+sin(a)sin(b) =0,06
cos(a-b) = 0,06
(a-b) = 86,56 gr.

Kortom ik kom hier niet uit na veel proberen
Bij voorbaat dank voor een advies
Joep

joep
Ouder - dinsdag 30 juni 2015

Antwoord

Hallo Joep,

Als ik het goed begrijp, gaat het om deze drie bekende krachten:



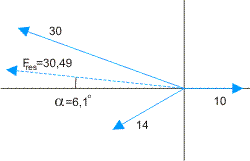
Wanneer we deze ontbinden in horizontale en verticale componenten en de componenten vervolgens optellen, vinden we de resulterende kracht:

F_res = (-30,32 ; 3,26)
|F_res| = 30,49
Tan(a) = ^3,26/_30,32 = 0,108, dus:
a=6,1°

Zover was je gekomen, begrijp ik. De vraag is nu om twee krachten te vinden met grootte 16 en 25, zodanig dat de som van de krachten nul is. Deze onbekende krachten moeten samen dus een tegengestelde resulterende kracht opleveren. Eén mogelijkheid heb ik hieronder getekend:



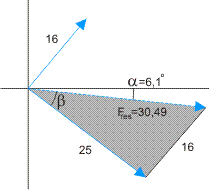
We bekijken de grijze driehoek. Met behulp van de cosinusregel kan hoek ß worden berekend. Er geldt:

16² = 25²+30,49² -2·25·30,49·cos(ß)
cos(ß)=0,852
ß=31,6°

De hoek tussen de horizontale as en F_res was al bekend (6,1°), dus hoek b (richting kracht van 25 t.o.v. horizontale as) is 31,6+6,1=37,7° (eigenlijk -37,7°, volgens afspraken over de positieve draairichting).

Op gelijksoortige wijze kan hoek a worden gevonden.

Er is nog een tweede oplossing: de krachten van 16 en 25 kunnen worden gespiegeld ten opzichte van de werklijn van F_res.

dinsdag 30 juni 2015

Re: Vector vergelijking

©2001-2024 WisFaq