Goniometrische vergelijking

Hallo,
Ik heb twijfels over een voorbeeld-uitwerking in mijn boek.

Los exact op:
sin(3x+2) = cos(2x)
Herschreven wordt dat cos(1/2$\pi$-(3x+2))=cos(2x).
Dat geeft A=B+k.2$\pi$ of A=-B+k.2$\pi$
In de uitwerking van A=B+k.2p
staat;
-3x-1+1/2$\pi$ = 2x+k.2$\pi$
-5x=1+1/2$\pi$+k.2$\pi$
x=-3/10$\pi$-1/2k.2/5$\pi$
Moet dat niet zijn;
x= -3/10-k.2/5$\pi$?
k.2$\pi$ delen door -5 lijkt mij -k.2/5$\pi$
Waar komt die halve k vandaan
gr edward

edward
Leerling bovenbouw havo-vwo - donderdag 5 februari 2015

Antwoord

't Is een rommeltje... Ik zou dat zo doen:

$
\eqalign{
& \sin (3x + 2) = \cos (2x) \cr
& \cos (\frac{1}
{2}\pi - (3x + 2)) = \cos (2x) \cr
& \frac{1}
{2}\pi - (3x + 2) = 2x + k \cdot 2\pi \vee \frac{1}
{2}\pi - (3x + 2) = - 2x + k \cdot 2\pi \cr
& - 3x - 2 + \frac{1}
{2}\pi = 2x + k \cdot 2\pi \vee - 3x - 2 + \frac{1}
{2}\pi = - 2x + k \cdot 2\pi \cr
& - 5x = 2 - \frac{1}
{2}\pi + k \cdot 2\pi \vee - x = 2 - \frac{1}
{2}\pi + k \cdot 2\pi \cr
& x = - \frac{2}
{5} + \frac{1}
{{10}}\pi - k \cdot \frac{2}
{5}\pi \vee x = - 2 + \frac{1}
{2}\pi - k \cdot 2\pi \cr
& x = - \frac{2}
{5} + \frac{1}
{{10}}\pi - k \cdot \frac{2}
{5}\pi \vee x = - 2 + \frac{1}
{2}\pi - k \cdot 2\pi \cr
& x = - \frac{2}
{5} + \frac{1}
{{10}}\pi + k \cdot \frac{2}
{5}\pi \vee x = - 2 + \frac{1}
{2}\pi + k \cdot 2\pi \cr
& x = \frac{{k \cdot 4\pi + \pi - 4}}
{{10}} \vee x = \frac{{k \cdot 4\pi + \pi - 4}}
{2} \cr}
$

Even een grafiekje?



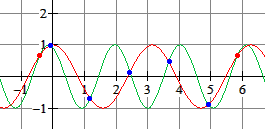
Is dat een antwoord op de vraag?

donderdag 5 februari 2015

©2001-2024 WisFaq