Statistiek en kansrekenen

Momenteel ben ik bezig met het schrijven van mijn scriptie. Ik heb statistische berekeningen nodig om mijn conclusies te kunnen onderbouwen. Mijn vraag is als volgt:

Mijn scriptie gaat faillissementsvoorspellingsmodellen. Er zijn model 1, 2 en 3. Ik wil bewijzen of de nauwkeurigheidspercentages van modellen beïnvloed worden door de periode van de steekproef(gemakshalve jaar 1 en jaar 2). De steekproefomvang is 21 bedrijven.

Model 1 heeft een nauwkeurigheidsperc. van 81% in jaar 1 (steekproef 1) en in jaar 2 is dit 72% (steekproef 2). Ik wil graag aantonen of de verschillen statistisch significant zijn (tussen jaar 1 en 2).

Ik vraag me af of het terecht is om de volgende statistische methode toe te passen, om te kunnen aantonen of de verschillen statistisch significant zijn.

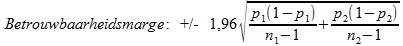(uitgaande van 95% betrouwbaarheid)

p₁= percentage uit jaar 1 (steekproef 1)
p₂= percentage uit jaar 2 (steekproef 2)

n1= steekproefomvang in jaar 1 (steekproef 1)
n2= steekproefomvang in jaar 2(steekproef 2)

Na het toepassen van de formule kom ik tot de volgende conclusie:


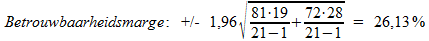
Verschil in p₁ en p₂ = 9%

Conclusie: verschil niet statisch significant (verschil p₁-p₂ moet groter zijn dan 26,13% wil het verschil significant zijn)

Bron: Voortgezette Statistiek voor Historici - STEEKPROEVEN EN STATISTISCHE TOETSEN

Mijn vraag is: Kan ik zomaar deze methode toepassen? Zo nee, wanneer kan het dan wel?

Alvast bedankt voor uw tijd!

Tang
Student hbo - maandag 7 juli 2014

Antwoord

Je hebt de beschreven methode correct toegepast, ik zou ook geen reden weten waarom dat hier niet zou mogen.

De conclusie is ook juist: het gevonden verschil is statistisch niet significant. Bedenk wel dat je hiermee niet automatisch hebt bewezen dat er geen verschil bestaat: je kunt een eventueel verschil statistisch niet onderbouwen.

maandag 7 juli 2014

Re: Statistiek en kansrekenen

©2001-2024 WisFaq