Ongelijkheid oplossen

Hallo meneer,

1) Ik heb paar video's gekeken en voorbeelden gezien over ongelijkheiden maar ik snap nog steeds niet wanneer ik $>$ of $<$ moet gebruiken.
Bijvoorbeeld bij: 2p+1$<$3p²+2p-4
Als antwoord heb ik 1,29 v -1,29 maar dan wanneer moet $<$ of $>$ gebruiken?

2) 12-$\frac{2}{3}$x$>$4x-7
Dit heb ik paar keer geprobeerd, maar ik kom uit x=7,1... en dat is fout.

saideh
Leerling bovenbouw havo-vwo - zondag 15 juni 2014

Antwoord

Bij 1) los je eerst de vergelijking 2p+1=3p²+2p-4 op. Je krijgt dan twee oplossingen:

$x=-\frac{1}{3}\sqrt{15}$ of $x=\frac{1}{3}\sqrt{15}$

Links staat een lineaire formule en rechts de formule van een dalparabool. Dat ziet er als grafiek zo uit:



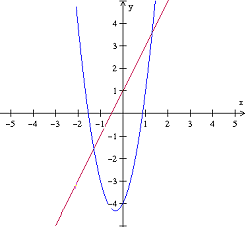
Welk 'gebied' moet je nu hebben? Daar waar de rode lijn kleiner is dan de blauwe parabool. De oplossing wordt:

$x$<$-\frac{1}{3}\sqrt{15}$ of $x$>$\frac{1}{3}\sqrt{15}$

Lineaire ongelijkheden kan je oplossen zoals je 'normaal' lineaire vergelijkingen oplost. Er is echter één addertjes onder het gras. Als je vermenigvuldigt of deelt door een negatief getal dan 'klapt het teken om'.

$
\begin{array}{l}
12 - \frac{2}{3}x > 4x - 7 \\
36 - 2x > 12x - 21 \\
- 14x > - 57 \\
x < \frac{{57}}{{14}} \\
\end{array}
$

Zo doe ik dat...

zondag 15 juni 2014

©2001-2024 WisFaq