
Zijde van een regelmatige achthoek
Hoe kun je bewijzen dat a=0,455√O klopt? (a= zijde achthoek, O= oppervlakte achthoek)
Merit
Leerling onderbouw vmbo-havo-vwo - donderdag 6 februari 2003
Antwoord
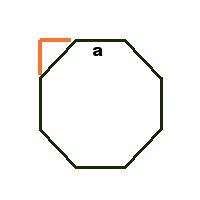
Redeneer vanuit de zijde van de achthoek. Die zijde is a=3.
Reken nu met de stelling van pythagoras uit wat de lengte van de oranje driehoekszijde is
Dat wordt dan 0,707106781·3 = 2,121320344
Teken ook de andere drie driehoekjes aan de achthoek.
Je krijgt dan een vierkant met lengte 2,121320344+3+2,121320344 = 7,242640687
En de oppervlakte van dat vierkant wordt 52,45584412
Voor de achthoek moet daar de oppervlakte van 4 driehoekjes af (4·1/2·2,1213203442 eraf):
Oppervlakte achthoek=52,45584412-4·2,25=43,45584412
Hier klopt de stelling dus.... maar dit was enkel voor het idee....... nu het echte bewijs met a in plaats van de 3.
lengte zijde achthoek = a
lengte zijde van het driehoekje wordt √(1/2a2)=a·√1/2
oppervlakte driekhoekje wordt 1/2·(a·√1/2)2=1/4a2
oppervlakte vier driehoekjes samen is dus a2
lengte zijde vierkant = a+2a·√1/2=a·(1+2√1/2)= 2,414213562a
oppervlakte vierkant = 5,828427125·a2
oppervlakte achthoek = 4,828427125·a2
√O=2,197368227a en klaar
Met vriendelijke groet
JaDeX

donderdag 6 februari 2003
 ©2001-2025 WisFaq
©2001-2025 WisFaq
|