Kromme in poolcoördinaten - oppervlakte en momenten

Beste,
Ik hou van wiskunde. Had er ook altijd groot succes in. Spijtig genoeg heb ik te weinig aantal uren wiskunde gehad in het secundair, wat betreft mijn momenteel gevolgde richting. Wat betreft onze huidige docent, is iemand die totaal geen zin heeft om les te geven. En die dat zelf toegeeft.

Ik zou graag het volgende willen weten:
Stel:
kromme
r=1+sin³(t/2)
is gegeven.

Met het stuk dat moet bepaald worden ligt tussen : y=0,75
en y=1,25 in het eerste kwadrant.

*De oppervlakte van de sector bepaald door het stuk kromme in het xy-vlak en voerstralen van de uiteinden van het stuk kromme naar de oorsprong.

*Laat het overeenkomstige stuk kromme in het ty-vlak wentelen om de t-as. En bepaal het moment om de t-as van het omwentellingsoppervlak.

*Bepaal de inhoud van het omwentelingslichaam dat ontstaat als men het overeenkomstige stuk kromme in het t,x vlak laat wentelen om de t-as

Isci
Student universiteit - zondag 2 februari 2003

Antwoord

Hoi,

Je hebt dus de vergelijking van een kromme in poolcoördinaten: r=1+sin³(t/2). t stelt de hoek met de X-as voor en r de afstand van de oorsprong. Je kan overgaan naar x-y-coördinaten: x=r.cos(t) en y=r.sin(t). sin(t) heeft periode 2p en sin(t/2) heeft dus periode 4p. We kunnen t dus beperken tot [0,4p].

Dit is de grafiek (met Excel) voor tÎ[0,4p]:




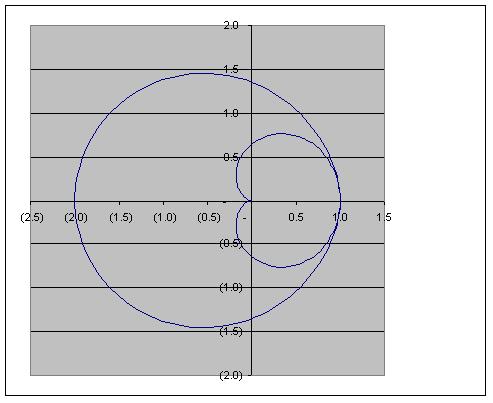
Zoals je ziet is het niet duidelijk wat er 'binnen' de kromme ligt tussen y-0.75 en y-1.25 binnen het 1ste kwadrant... De binnenste 'hartkromme' krijgen we voor t in [2p,4p], de buitenste voor t in [0,2p]. De opgave heeft enkel zin wanneer we ons beperken tot [0,2p]. We krijgen dan:




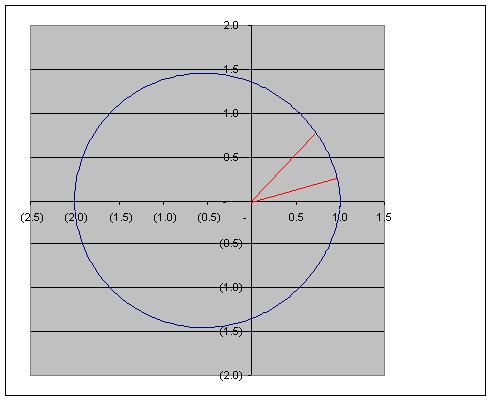
Om te weten welke t er bij y=0.75 hoort, moeten we dus t halen uit 0.75=r.sin(t)=(1+sin³(t/2)).sin(t). We hebben dit bij t₀=0.789. Het zelfde moeten we doen voor y=1.75. Dit is voor t₁=1.401. Deze waarden werden numerisch berekend...

Je vragen dan:
Oppervlakte van het segment
Bij dt hoort een sectortje met oppervlakt r².dt/2. Je moet dus Int(r²/2,t=t₀..t₁) berekenen... Wellicht moet dit ook numerisch.

Moment om T-as in Y-T-vlak
Je hebt: y=r.sin(t)=(1+sin³(t/2)).sin(t). Het n-de graadsmoment tov de T-as is gegeven door Int(tⁿ.y,t=0..2p). Het lijkt me niet doenbaar om dit uit te rekenen...

Moment om T-as in X-T-vlak
Je hebt: x=r.cos(t)=(1+sin³(t/2)).cos(t). Het n-de graadsmoment tov de T-as is gegeven door Int(tⁿ.x,t=0..2p). Het lijkt me evenmin doenbaar om dit uit te rekenen...

Dit lijkt me heel een bizarre opgave, vooral omdat T met X en Y gemixt wordt...

Groetjes,
Johan

andros
woensdag 5 februari 2003

©2001-2024 WisFaq