Oppervlakte tussen twee functies en x-as door middel van integreren

Hoi,
Ik zit al een tijdje vast op een opgave en ik heb veel geprobeerd maar kom er echt niet uit..

Gegeven zijn de functies f(x)=x en g(x)=√x+2
De grafieken van beide functies en de x-as sluiten een gebied in. Bereken de oppervlakte van dit gebied door middel van integreren. (er zijn meerdere integralen)

Als eerst heb ik geprobeerd om √x+2 = x op te lossen.
x+2=x² $\rightarrow$ x²-x-2=0. ABC formule en ik kom uit op x=2 en x=-1. Als ik het plot zie ik dat -1 geen goede antwoord is, maar x=2 wel. Dit vond ik raar, want ik heb de abc formule precies gebruikt hoe hij moet en geen slordigheidsfoutjes gemaakt.

Volgens de antwoordenboek is er een oppervlakte tussen -2 en 0 en tussen 0 en 2 en die oppervlaktes moet je dan optellen.

Ik snap echt niet wat ik verkeerd doe,
Alvast hartelijk bedankt voor het antwoorden!

Groetjes,
Alex.

Alex
Leerling bovenbouw havo-vwo - maandag 2 december 2013

Antwoord

Beste Alex,

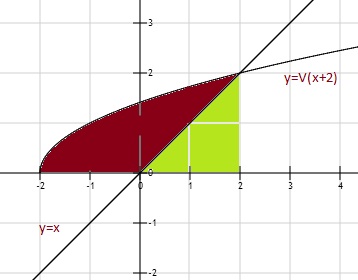
Het ingesloten gebied is het rode gebied.
Welnu rood+groen-groen=rood.

Probeer eerst eens de integraal te berekenen van:
$
\int\limits_{ - 2}^2 {\sqrt {x + 2} }\,dx
$

Dit is dus rood+groen.

Hier haal je dan vervolgens "groen" weer vanaf.
groen = $
\int\limits_0^2 x\,dx
$

DvL
maandag 2 december 2013

Re: Oppervlakte tussen twee functies en x-as door middel van integreren

©2001-2024 WisFaq