
Congruente driehoeken
Twee driehoeken zijn congruent als paarsgewijs een zijde, het hoogtelijnstuk en het zwaartelijnstuk naar die zijde even lang zijn. Bewijs dit.
Sümeyy
Student Hoger Onderwijs België - vrijdag 29 november 2013
Antwoord
Beste Sumeyye,
We zullen eens zien.
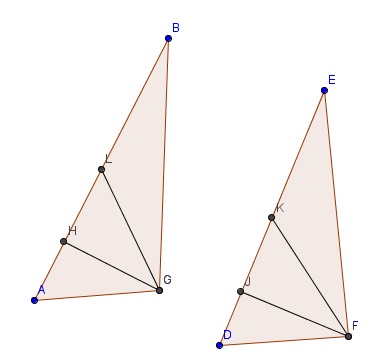
$
\begin{array}{l}
\\
\left\{ \begin{array}{l}
GH = JF \\
\angle GHL = FJK = \bot \\
GL = KF \\
\end{array} \right\} \Rightarrow HL = JK(pythagoras) \\
\left\{ \begin{array}{l}
AB = DE \\
HL = JK \\
LB = KE \\
\end{array} \right\} \Rightarrow AH = DJ \\
\left\{ \begin{array}{l}
AH = DJ \\
GH = FJ \\
\angle AHG = DJF = \bot \\
\end{array} \right\} \Rightarrow AG = DF \\
\\
\left\{ \begin{array}{l}
GH = FJ \\
AH = DJ \\
AG = DF \\
\angle AHG = DJF = \bot \\
\end{array} \right\}zzz \Rightarrow AGH = DFJ \Rightarrow \angle A = \angle D \\
\left\{ \begin{array}{l}
AB = DE \\
AG = DF \\
\angle A = \angle D \\
\end{array} \right\} \Rightarrow zhz \\
\end{array}
$
De vraag is nu of dit ook geldt wanneer de hoogtelijn buiten de driehoek valt?
Dit laat ik aan u over, maar voor de volledigheid zou dit ook bewezen moeten worden.
mvg DvL
DvL
vrijdag 29 november 2013
 ©2001-2024 WisFaq
©2001-2024 WisFaq
|