Bewijs voor de oppervlakte van een cirkel

Hoe kan je bewijzen dat de oppervlakte van een cirkel $\pi r^{2}$ is? Bij mijn weten is het onmogelijk.

Thomas
2de graad ASO - donderdag 23 januari 2003

Antwoord

Beste Thomas,

Om het echt te kunnen bewijzen zul je bekend moeten zijn met integreren, maar ik zal proberen het je duidelijk te maken m.b.v. de rechthoekjesmethode (die wordt ook gebruikt als 'opstap' naar het integreren).

Beschouw een halve cirkel (alleen positieve functiewaardes, dus boven de x-as). Om daar het functievoorschrift van op te stellen kun je een willekeurig punt op de cirkel kiezen. Noem dit punt P(x,y). Laat nu vanuit dit punt een loodlijn op de x-as en noem dit punt R, en vanuit het punt P laat je ook een loodlijn op de y-as hiervan noem je het snijpunt Q. Verbind het punt P met de oorsprong en er ontstaat een rechthoekige driehoek ORP. Hiervan is de schuine zijde OP, de x-waarde van het punt P is |OR| en de y-waarde van het punt P is |OQ|. De straal van de cirkel is de schuine zijde en indien je die weet kun je het functievoorschrift van de halve cirkel opstellen a.d.h.v. Pythagoras.

Neem voor een cirkel straal 1, dus |OP| = 1. Pythagoras zegt nu de schuine zijde² = som van de rechthoekzijdes², dus hier 1² = |PR|² + |OR|² oftewel 1 = y² + x² en bijgevolg is y² = 1 - x² en is het functievoorschrift voor de halve cirkel y = √(1 - x²).

Om hier nu de oppervlakte te bepalen kun je gebruik maken van de rechthoekjesmethode. Die werkt als volgt : je neemt op een gekozen interval een aantal deelintervallen, en die deelintervallen hebben allemaal dezelfde breedte (namelijk de plaats die ze innemen op de x-as) en een hoogte (bijhorende snijpunt aan de grafiek). Oppervlakte rechthoek is breedte × hoogte. En deze procedure herhalen geeft een goede benadering van de oppervlakte.

Hier toegepast. Beschouw het interval [-1,1] en verdeel het interval in laten we zeggen 50 deelintervallen. Dan is de breedte van elk deelinterval 2/50 = 0,04. We nemen van elke rechthoek het klassenmidden want dat geeft een betere benadering dan de onder- of bovensom. Je krijgt dus voor het eerste deelinterval (-1 + (-1 + 0,04)) : 2 = -0,98. Dus de oppervlakte van het eerste deelinterval is 0,04 × f(-0,98) $\approx$ 0,007959899496. En je herhaalt dit totdat je het 50^ste deelinterval gehad hebt.

Gelukkig gaat het via een computerprogramma veel sneller dan met de hand, Maple gaf als uitkomst 1,570811728 als oppervlakte van de halve cirkel op het interval [-1,1] met 50 deelintervallen. Natuurlijk kun je het aantal deelintervallen vergroten wat er voor zorgt dat er een meer nauwkeurige uitkomst uitkomt. Voor 10 000 deelintervallen gaf Maple 1,570796814 dus zoveel scheelt het niet.



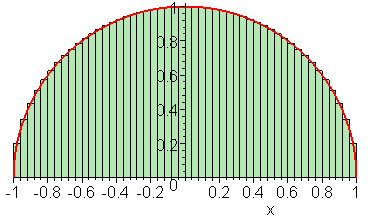
Maar dat was de oppervlakte van de halve cirkel, dus is de oppervlakte van de hele cirkel het dubbele, dus ongeveer 3,141593628... en is bijna $\pi$! Maar dat was voor een cirkel met straal 1, en aangezien 1² = 1 kwam dit mooi uit, maar hiermee hebben we de algemene formule nog niet.

Indien je dezelfde manier als hierboven beschreven toepast voor straal = 2. Dan wordt het functievoorschrift van de halve cirkel y = √(4 - x²) en nu is het interval [-2,2] en indien we dan 50 deelintervallen nemen is de breedte van elk deelinterval 4/50 = 0,08 en is dus minder nauwkeurig. Laten we 100 deelintervallen nemen 4/100 = 0,04 en hiermee is de breedte van elk rechthoekje gelijk aan die van de vorige.

Dus is de benaderde oppervlakte van de halve cirkel ongeveer 6,285131104 dus de hele cirkel heeft als oppervlakte 12,57026221 en laten we dit eens delen door de oppervlakte die we eerst hadden berekend. Dan kom je ongeveer op 4 uit. Indien je halve cirkel met straal 3 neemt dan heeft de hele cirkel bij benadering als oppervlakte 28,27... en dit gedeeld door de oppervlakte die we uitkwamen van de cirkel met straal 1 is 9.

Indien je dit blijft herhalen zul je zien dat er telkens het kwadraat van de straal uitkomt. Er is dus één getal waarmee het kwadraat van de straal vermenigvuldigd moet worden om de oppervlakte van een cirkel te berekenen.
En dat getal heeft men $\pi$ genoemd en is ongeveer gelijk aan 3,141592654... en kan dus berekend worden met de volgende integraal



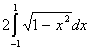
Pi is trouwens irrationaal, dat wil zeggen pi heeft oneindig veel decimalen en hierin zit geen vast patroon (geen periode). Dit kun je ook afleiden uit de berekening m.b.v. de integraal, want deze methode verdeelt het interval in oneindig veel rechthoekjes waardoor de breedte van elk deelinterval bijna 0 wordt, dus je kunt $\pi$ niet precies uitrekenen, derhalve met je werken met een goede benadering.

Is je vraag duidelijk beantwoord zo? Ik ben altijd bereid op eventuele vragen te antwoorden.

PS: Het volgende plaatje van Dhr. De Moudt maakt het geheel nog duidelijker:



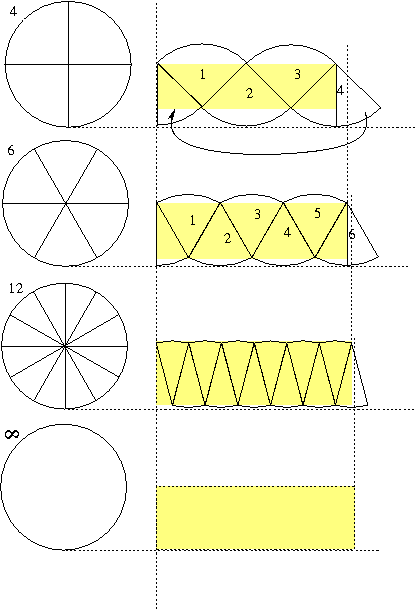
Groetjes,

donderdag 23 januari 2003

©2001-2024 WisFaq