Gelijkbenigheid bewijzen

Op school heb ik de volgende opgave gekregen:

Gegeven zijn twee cirkels met gelijke straal die elkaar snijden in punt A en B. De lijn l gaat door A en snijdt de cirkels in P en Q. Bewijs dat driehoek BPQ gelijkbenig is.

Nu loop ik bij het bewijzen hiervan een beetje vast.
Wat ik tot nu toe heb bedacht:

Door in m'n gedachten de rechter cirkel wat naar rechts te verplaatsen, blijven volgens mij BQ en PB even lang. Dus dan zou bewezen moeten worden dat QPB=QBP?

AQB staat op de grote boog AB in de rechtercirkel en APB staat op de kleine boog AB in de linkercirkel.

Hoe kan ik hiermee verder? Alvast bedankt

Johnny
Leerling bovenbouw havo-vwo - donderdag 29 maart 2012

Antwoord

Dag Johnny,
Je bent op de goede weg.
Je moet inderdaad proberen te bewijzen dat de hoeken P en Q in driehoek BPQ aan elkaar gelijk zijn.

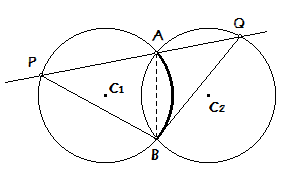
En je moet, goed gezien, gebruik maken van omtrekshoeken op beide cirkels.
Hoek P staat op boog AB van cirkel C₁, hoek Q staat op boog AB van cirkel C₂; zie bovenstaand plaatje.
En dan moet je (zelf) nog bewijzen dat die (beide KLEINE) bogen gelijk zijn (gelijke lengte hebben).
En dat zal je, omdat je weet dat de stralen van beide cirkels gelijk zijn, wel lukken, denk ik.
Tip: wat weet je van de hoeken AC₁B en AC₂B?

donderdag 29 maart 2012

Re: Gelijkbenigheid bewijzen

©2001-2024 WisFaq