Secans en cosecansfunctie

ik moet de nulpunten en periode van deze 2 functies berekenen maar wete niet hoe eraan te beginne

gerthe
Iets anders - donderdag 9 januari 2003

Antwoord

Beste Gert,

Hieronder heb ik de secans-grafiek geplot.



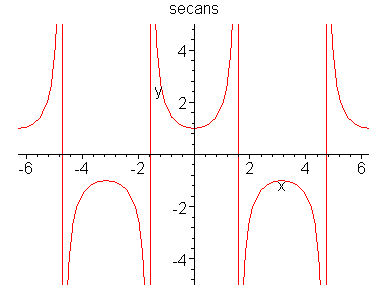
Die verticale rode lijnen geven aan dat de functie daar niet bestaat (zo'n lijn noem je een verticale asymptoot).
Je kunt de secansfunctie schrijven als sec(x) = 1/cos(x).
Wanneer is een functie onbepaald? In een breuk is dat als er gedeeld wordt door 0, m.a.w. wanneer is cos(x) = 0.
Om daar een antwoord op te krijgen, kun je de cosinus-functie plotten en de nulpunten uit de grafiek afleiden, maar je kunt ook de goniometrische cirkel (= eenheidscirkel) bekijken. In beide gevallen kom je tot de conclusie dat cos(x) = 0 Û x = kp/2 met als voorwaarden kÎ en k oneven. Dus voor die waarden is de secans-functie niet gedefinieerd. De periode van de cosinusfunctie is 2p dus ook voor de secansfunctie.

Dan de cosecansfunctie. Die functie kun je schrijven als 1/sin(x). Hieronder vind je grafiek van de cosecansfunctie.



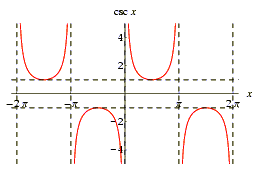
Hiervoor geldt hetzelfde als voor de secansfunctie. Alleen zijn de verticale asymptoten hier voor sin(x) = 0.
Om sin(x) = 0 op te lossen kun je wederom gebruik maken van de eenheidscirkel, of de grafiek van sin(x) te plotten.
Je zult uitkomen dat dit geldt voor x = kp, kÎ.
Dus voor die waardes bestaat de secansfunctie ook niet.
De periode van de sinusfunctie is 2p, dus ook voor de secans. Wat de nulpunten betreft : die zijn er niet!Want wat zijn nulpunten? Nulpunten zijn x-waarden (punten op grafiek) waarvoor geldt dat de functiewaarde = 0 (oftewel y = 0 ook f(x) = 0).Een functie van de gedaante 1/x wordt nooit 0, plot die functie maar 'ns, je zult zien dat de functie wel naar 0 toe 'kruipt', maar hij wordt het nooit. Er is namelijk een horizontale asymptoot y = 0 (dat wil zeggen, alleen als je met limieten gaat werken, zal +oneindig en -oneindig ervoor zorgen dat 1/x 0 wordt).

Ik hoop dat 't nu wat duidelijker is, anders dan hoor ik 't wel,

Groetjes,

donderdag 9 januari 2003

©2001-2024 WisFaq