Re: Re: Hoe werkt een arcsinus?

Dit is een reactie op vraag 63760

Mijn dank. De code is me duidelijk: verifieer de input (r=-1 en r =1) en neem 2 tussendoortjes (r=1 en -1). Het venijn zit em in de staart: ArcSin:=ArcTan(r/SQRT(-r*r+1)). Omdat ik er nog wat van wil leren: Kun je dit uitleggen? Welke achtergrondkennis had ik moeten hebben om dit zelf te verzinnen?

Willem
Iets anders - woensdag 15 december 2010

Antwoord

Het lijkt ingewikkelder dan het is, denk ik.



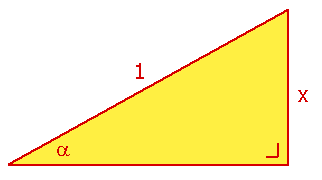
In de driehoek geldt:

$
\eqalign{
& \sin \alpha = x \Rightarrow \alpha = \arcsin \left( x \right) \cr
& \tan \alpha = \frac{x}
{{\sqrt {1 - x^2 } }} \Rightarrow \tan \left( {\arcsin \left( x \right)} \right) = \frac{x}
{{\sqrt {1 - x^2 } }} \Rightarrow \cr
& \arcsin \left( x \right) = \arctan \left( {\frac{x}
{{\sqrt {1 - x^2 } }}} \right) \cr}
$

De arccos(..) zal dan wel op dezelfde manier gaan maar dan anders...

woensdag 15 december 2010

©2001-2024 WisFaq