Lognormale verdeling

Ik heb de volgende vraag; X is normaalverdeeld onder parameters mu en variantie sigmakwadraat, Y = e tot de macht x. Bepaal de dichtheid van Y (met als tip: de verdeling van Y heet lognormaal verdeeld)

De vraag: X is verdeeld onder MU en variantie sigmakwadraat. Y is e tot de macht X. Bepaal de dichtheid van Y, en vooral snap ik niet hoe je tot deze dichtheid komt?
BVD

rob
Student universiteit - zaterdag 4 januari 2003

Antwoord

Als de stochast X Normaal verdeeld is met verwachting m en variantie s² dan kunnen we de verdelings functie van de stochast Y, gedefinieerd door Y = e^X vinden via de verdelingsfunctie van X. Dat gaat zo:

De verdelingsfunctie G van Y is gedefinieerd door G(y) = P(Y y). Vul in, Y = e^X, dan krijg je:

G(y) = P(e^X y) = P(X log y), want e^X y alleen als X log y .

Omdat X normaal verdeeld is, geldt:
P(X u ) = F((u - m)/s). Hierbij is F dan de standaard normale verdelingsfunctie, (die als dichtheidsfunctie f =
F' heeft :



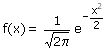
We hebben dus: G(y) = P( X log y) = F((log y - m)/s).

De dichtheidsfunctie van Y kunnen we vervolgens vinden door
differentieren (kettingregel gebruiken!):



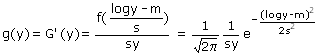
(alles voor y > 0 natuurlijk)

JCS
woensdag 8 januari 2003

©2001-2024 WisFaq