Re: Constructie parabool

Dit is een reactie op vraag 63527

Bewijs...?

Daaf S
Docent - vrijdag 12 november 2010

Antwoord

Dag Daaf, Je hebt de spelregels toch wel gelezen?
Ik herhaal de eerste constructiestappen nog even.

Uitgaande van een parabool met top O en vergelijking y = ax², waarop het punt P = (t, at²) ligt (in een assenstelsel dus).
1. Trek een lijn door P evenwijdig aan de as (dus aan de y-as).
2. Teken het lijnstuk OP.
3. Construeer de loodlijn op OP in het punt O.
4. Bepaal het snijpunt P' van de lijnen van stap 1 en 3.
5. Construeer de lijn i door P' loodrecht op de as (de y-as).
Dan heb je iets als in onderstaande figuur.

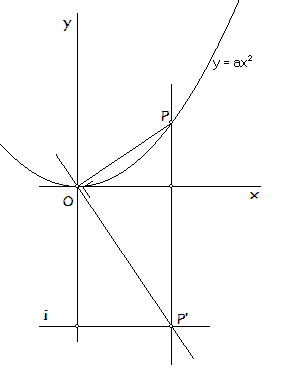
Nu is rico(OP) = at²/t = at (toename y gedeeld door toename x).
En dan is rico(OP') = -1/(at). (*)
Is u = y(P'), dan geldt ook: rico(OP') = u/t, want x(P') = x(P) = t.
Dus: u/t = -1/(at), en dan is u = -1/a.
Het bij P geconstrueerde punt P' ligt dus altijd op de lijn i (evenwijdig aan de x-as) met vergelijking y = -1/a. Dwz.:
de lijn i is onafhankelijk van de plaats van P op de parabool.

(*) Hier is de eigenschap gebruikt dat het product van de rico's van twee lijnen die loodrecht op elkaar staan, gelijk is aan -1.

Willen we nu een ander punt Q op de parabool construeren, dan kan dat met de volgende stappen:
6. Kies een punt Q' op de lijn i.
7. Trek Q'O.
8. Construeer de lijn door Q' evenwijdig aan de as.
9. Construeer de loodlijn op Q'O in het punt O.
10. Het snijpunt van de lijnen van stap 8 en 9 is Q.

Het punt Q ligt inderdaad op de parabool. De rol van Q en Q' is immers dezelfde als die van P en P'.
En, je hebt geen x- en y-as meer nodig. Het kan dus ook met een parabool die scheef staat. Zie onderstaande figuur.


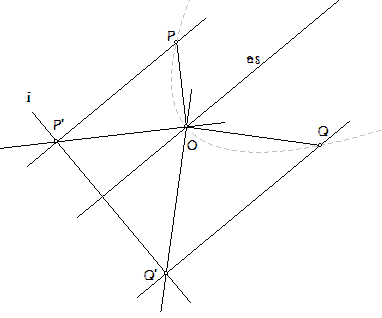
Ik denk dat aan je 'verzoek' om een bewijs zo wel voldaan is.

vrijdag 12 november 2010

©2001-2024 WisFaq