Re: Limieten van goniometrische functies met cosinus

Dit is een reactie op vraag 63432

hallo,

ik heb teller en noemer vermenigvuldigd met (1+cos(5x)).(cos(7x)+1)

en na het uit te werken, kom ik het volgende uit :
[cos(7x)+ sin²(5x)-cos²(5x).cos(7x)]/[-sin²(7x)+cos²(7x).cos(5x)-cos(5x)]

ik zou niet weten hoe ik dit verder kan uitwerken zodat ik alleen sin²(5x) overhoud in de teller en sin²(7x) in de noemer.

groetjes,

Tamara
3de graad ASO - zondag 31 oktober 2010

Antwoord

In de teller wordt:
(1-cos(5x))(1+cos(5x)) = 1-cos²(5x) = sin²(5x)
In de noemer wordt:
(cos(7x)-1)(cos(7x)+1) = cos²(7x)-1 = -sin²(7x)
Je bekomt dan :



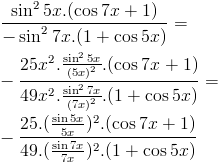
Lukt het nu verder?

zondag 31 oktober 2010

©2001-2024 WisFaq