Re: Raakvlak

Dit is een reactie op vraag 62864

Dag Thijs,
Ik ben aan het meevolgen op deze interessante vraag en begrijp het ook grotendeels. Maar de normaalvector
(2,1,2)^T moet je mij nog eens uitleggen...
Kan dat ?
Prettige zondag verder,
Rik

Rik Le
Iets anders - zondag 25 juli 2010

Antwoord

Dag Rik,

In dit antwoord probeer ik twee dingen uit te leggen:
1) Wat is een vector?
2) Waarom zo'n verband tussen een normaalvector en een vlakvergelijking.

1) Wat is een vector?
Een vector is een soort pijl van een punt naar een ander punt. deze vector geeft de richting en de afstand aan tussen de twee punten. Zo'n vector wordt genoteerd als 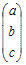. Om typografische redenen wordt zo'n vector ook vaak horizontaal genoteerd: (a b c)^T. Die 'T' staat dan voor 'Transposed' (Nederlands: 'Getransponeerd'). Deze vector geeft het volgende aan:
Om van het ene punt naar het andere punt te komen moet je:
a in de x-richting
b in de y-richting
c in de z-richting.

Voorbeeld: Vector P naar Q bij gegeven punten P(2,5,3) en Q(6,2,3).
Van 2 naar 6 $\to$ 4
Van 5 naar 2 $\to$ -3
Van 3 naar 3 $\to$ 0
Vector van P naar Q: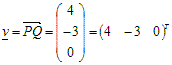

De afstand tussen twee punten is dan: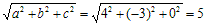

2) Waarom zo'n verband tussen een normaalvector en een vlakvergelijking.

Een vlak heeft minimaal twee richtingsvectoren (je hebt twee richtingen nodig om een vlak te vormen). Als je een vector vindt die op beide richtingsvectoren loodrecht staat, dan staat die vector automatisch loodrecht op het gehele vlak. Om die twee richtingsvectoren te vinden moet je eerst drie punten A, B en C vinden die aan de vergelijking voldoen. Dan kun je twee richtingsvectoren (bijvoorbeeld van A naar B en van A naar C) Als een vector loodrecht staat op een vlak (of op een lijn bij de vlakke meetkunde), dan noemen ze dat de normaalvector van dat vlak. Een voorbeeld:

vlakvergelijking: 15x+20y+12z=60
Drie punten: A(4,0,0), B(0,3,0), C(0,0,5)
Richtingsvector 1 = Vector AB = (-4 3 0)^T
Richtingsvector 2 = Vector AC = (-4 0 5)^T
Gezochte normaalvector = (a b c)^T

Twee vectoren staan loodrecht op elkaar, als hun inproduct 0 is (Dit is zo). Zo kun je een stelsel vergelijkingen op gaan lossen:



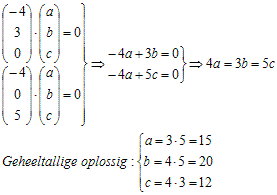
Het is geen toeval deze normaalvector (15 20 12)^T precies de zelfde getallen heeft als de vlakvergelijking.

Vandaar, als ik een normaalvector van een vlak heb en een punt in dat vlak, dan kan ik zonder veel rekenwerk de vlakvergelijking bepalen.

Hoop dat ik het idee van de normaalvector iets heb kunnen verduidelijken? Het is moeilijk in te schatten welke voorkennis ik mag gebruiken

Mvg Thijs Bouten

zondag 25 juli 2010

©2001-2024 WisFaq