Hoe maak je een even tovervierkant?

Hoe maak je nou een even vierkant? Ik las dat er alleen een algoritme bestaat voor een oneven vierkant, dus die is wel heel makkelijk te maken. Is het dus zo dat voor even vierkanten het voor elke afmeting anders is hoe die is in te vullen? dus zeg maar, een 4x4 vierkant verschilt qua regels met maken van een 20 bij 20 vierkant?

Truus
Leerling onderbouw vmbo-havo-vwo - dinsdag 22 april 2003

Antwoord

Beste Truus,

Ik heb twee methoden kunnen vinden. De eerste is geschikt voor vierkanten die als orde een viervoud hebben. De orde is de afmeting van het vierkant. De tweede methode is voor even orde die geen viervoud zijn.

Eerst hebben we nog wat meer basis begrippen nodig.

Basisbegrippen

We noemen de afmeting van een magisch vierkant dus de orde.

De constante van een magisch vierkant is de som van de kolommen, de rijen en de diagonaal. Ga maar eens na dat voor orde N: constant = ¹/₂(N³+N).

We noemen een magisch vierkant standaard als zij de getallen 1 tot en met N² bevat.

Een zeer bekend standaard vierkant van de orde 3 is "lo-shu" (afkomstig uit de Chinese overlevering)

Methode voor viervouden: diagonale methode

De volgende methode kan worden gerbuikt voor vierkanten van de orde die een veelvoud zijn van 4. Deze methode levert zelfs twee verschillende magische vierkanten op. Laten we beginnen met een vierkant van 4x4. Vul dit vierkant eerst met de getallen 1 tot en met 16. Teken dan de twee diagonalen.

Nu zijn er twee manieren om aan een magisch vierkant te komen. Je kunt de getallen op de diagonaal verwisselen of alleen de getallen die niet op de diagonaal staan. Je wisselt dan de getallen die symmetrisch zijn ten opzichte van het midden van het vierkant.



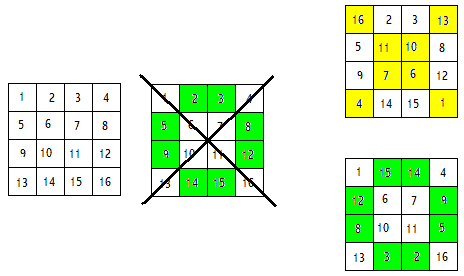
Zie Methode voor viervouden: diagonale methode voor een uitbreiding naar 8x8.

Methode voor even orde die geen viervouden zijn: methode van Strachey

Deze methode is wel wat ingewikkelder. De methode bestaat uit twee delen. Je begint met het maken van een vierkant dat is opgebouwd uit vier magische vierkanten.

In het tweede deel moet je dan nog een aantal getallen verwisselen om het gewenste magische vierkant te vinden.

Eerste deel van de methode van Strachey

Verdeel het vierkant in vier gelijke delen. Vul het linker boven vierkant met een standaard magisch vierkant van het juiste formaat.

Vul dan het rechter onder vierkant met hetzelfde standaardvierkant maar nu elk getal verhoogd met ¹/₄N².

Het vierkant rechts boven wordt gevuld met het standaardvierkant vermeerderd met ¹/₂ N². En het vierkant links onder wordt gevuld met het standaard vierkant vermeerderd met ³/₄N².

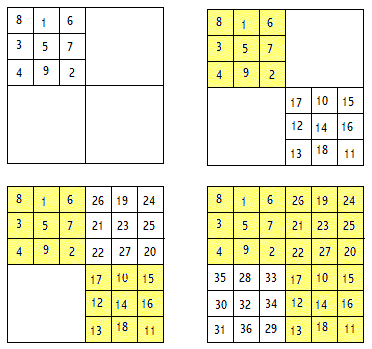
Tweede deel van de methode van Strachey

Nu moet je nog getallen in deze vierkanten met elkaar verwisselen. Het is wat moeilijk om dit met woorden uit te leggen. Ik doe toch een poging, maar de tekening hieronder maakt misschien wel meer duidelijk.

Eerst moet bepaald worden welke getallen van plaats zullen verwisselen. Deel de orde van het vierkant door 4. Dit bepaalt het aantal kolommen vanaf links dat wordt verplaatst. Het aantal kolommen rechts is dit aantal min 1. Verdeel dan het vierkant in een bovenhelft en een onder helft. Nu moet de selectie van de middelste rijen van deze twee helften 1 naar rechts worden geschoven.

De gekleurde vlakken in de volgende voorbeelden geven aan welke getallen zullen worden verwisseld.




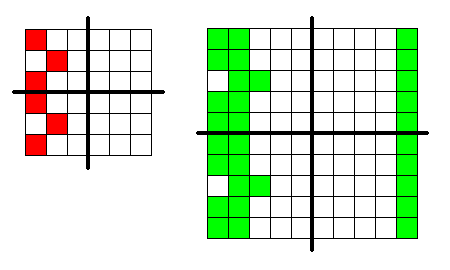
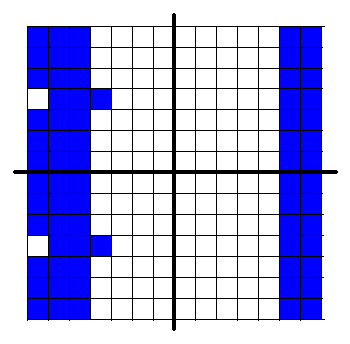
Wissel nu de geselecteerde getallen van de boven en onder helft.



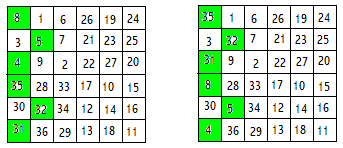
Je hebt nu twee methoden. Eentje als je orde een viervoud is (4,8,...) en een andere als de even orde dat niet is (6,10,..)

Probeer de vierkanten nu ook maar eens zelf te maken met de beschreven methode.

Het kan ook erg interessant zijn om uit te zoeken waarom deze methoden eigenlijk werken.

Veel succes!! en natuurlijk veel plezier!!

Hieronder vind je ook nog een ander antwoord waar ook een manier wordt beschreven om even magische vierkanten te maken.

Zie Magische vierkanten vergroten

vrijdag 25 april 2003

©2001-2024 WisFaq