Faculteit en nCr

1. wat is precies het verband tussen nCr en faculteit? (kunnen ze ipv elkaar?)
bij de vraag : "als je 3 knikkers trekt uit een vaas van (3x wit, 2x rood, 1x blauw) wat is de kans op 3 verschillenden kleuren?
dit kan je op 2 manieren oplossen (volgens mij):
1. vaasmodel
2. uitschrijven (over deze gaat mijn vraag) \
het antwoord was volgens mij lerares:
3! x 3/6 x 1/5 x 2/4 = 0,3
2. maar faculteit kun je toch ook vervangen voor nCr? maar als ik 6 nCr 3 doe komt daar geen 6 uit.
3. en waarom kan je zomaar 3! doen en niet : n!/r!x(n-r)!?
4. en wanneer doe je vaasmodel en wanneer dit?
Alvast heel erg bedankt

merien
Leerling bovenbouw havo-vwo - zaterdag 22 mei 2010

Antwoord

Op 3. Aanpak van telproblemen kan je een overzichtje vinden van belangrijke telproblemen.

Die 'faculteit' kom je tegen bij faculteitsbomen. Hoeveel volgordes kan je maken van n (verschillende) objecten? Antwoord: n! Dit zijn permutaties.

Combinaties gebruik je als de volgorde er niet toe doet. Dat is dus wel iets anders dan wat jij 'faculteiten' noemt.

Maar laten we maar 's naar je voorbeeld kijken:

Als je (zonder terugleggen!) 3 knikkers trekt uit een vaas van (3x wit, 2x rood, 1x blauw) wat is de kans op 3 verschillenden kleuren?

De eerste manier is om de kans op 殚n bepaalde volgorde te berekenen en die kans dan te vermenigvuldigen met het aantal volgordes (=permutaties!) die je kan maken!



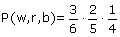
Hoeveel volgordes kan je maken met een witte, een rode en een blauwe knikker? Dat is een permutatie met 3 elementen. Dus 3! manieren...



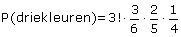
Die verschillende volgordes van die drie knikker zijn permutaties! De volgorde is daarbij juist wel belangrijk. Je kunt het ook nog eenvoudiger opvatten als: 'je hebt drie bakjes en drie knikkers, bij de eerste knikker kan je kiezen uit 3 bakjes, bij de tweede uit 2, ... dus 3򈭽=3!

Wat bedoel je precies met vaasmodel?

Zie ook 1. E閚 vraag - drie uitwerkingen.

zondag 23 mei 2010

©2001-2024 WisFaq