Berekening zijden 1 zijde bekend en drie hoeken

1 rechthoekzijde = 60 cm langste zijde
1 recht hoekzijde = onbekend dus gevraagd
1 schuine zijde = onbekend dus gevraagd
hoeken 90 graden, 86 graden en 4 graden

Hoe lang zijn de beide niet bekende zijden ??

Jan Ge
Iets anders - maandag 3 augustus 2009

Antwoord

Beste Jan,

Eerst maar eens een tekening maken met alle mogelijke situaties.

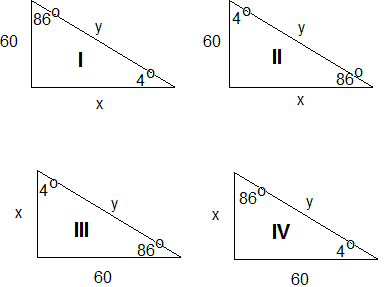
De vraag is nu: hoe groot zijn x en y bij driehoeken I, II, III en IV.

Driehoek I
Als je vanuit de 86°-hoek kijkt dan is de x de overstaande rechthoekszijde, en je kent de aanliggende zijde die is 60. Dus dan gebruik je de tangens van 86°, want tan(hoek) = ^{overstaande rechthoekszijde}/_{aanliggende rechthoekszijde}.
Hier tan(86°) = ^x/₆₀. Je kunt tan(86°) met een rekenmachine berekenen, da's ongeveer 14,3. Dus moeten we 14,3 = ^x/₆₀ oplossen. Dan is x = 14,3·60 858.

Om y te berekenen kun je de 4° of 86°-hoek kiezen, want we hebben x zojuist berekend. y is de schuine zijde (= hypotenusa) en t.o.v. 86°-hoek is 60 de aanliggende rechthoekszijde. Aangezien we met schuine zijde en aanliggende rechthoekszijde werken, moeten we de cosinus gebruiken, aangezien cos(hoek) = ^{aanliggende rechthoekszijde}/_{schuine zijde}.
Hier cos(86°) = ⁶⁰/_y. Dus is y = ⁶⁰/_cos(86°) ⁶⁰/_0,0698 860.

Probeer nu zelf bij driehoek II, III en IV de x en de y te berekenen. En dan zou je iets moeten opvallen als je driehoek I met III, en II met IV vergelijkt (en hoe zou je dit kunnen verklaren? Tip).
Je mag ook gebruik maken van de sinus, waarbij sin(hoek) = ^{overstaande rechthoekszijde}/_{schuine zijde}.
Het ezelsbruggetje SOS CAS TOA helpt je om de formules te onthouden, waarbij de eerste letter aangeeft of je sinus, cosinus of tangens te maken hebt, en de laatste twee letters geven aan door welke zijden te moet delen.

Mocht je vastlopen, reageer gerust.

Gr. Davy.

dinsdag 4 augustus 2009

©2001-2024 WisFaq