Trekken van kaarten

Uit een spel van 52 kaarten trekken we tegelijkertijd en op aselecte wijze 4 kaarten. Bereken de kans:
a) dat het 4 schoppen zijn
b) dat het 2 heren en 2 vrouwen zijn

Dit heb ik al:

a) Volgens een welbepaalde redenering
Kans op schoppen1: P1 = 1/4
Kans op schoppen2: P2 = 12/51
Kans op schoppen3: P3 = 11/50
Kans op schoppen4: P4 = 10/49
-----------------------------
Gemeenschappelijke kans: P = P1.P2.P3.P4 = 11/4165
Deze uitkomst lijkt te kloppen met wat vanachter in het boek staat.

b) Ik probeerde dezelfde methode toe te passen bij b, maar om de een of andere reden klopt dit niet.

Kans op heer1: P1 = 4/52
Kans op heer2: P2 = 3/51
Kans op dame1: P3 = 4/50
Kans op dame2: P4 = 3/49
------------------------
Gemeenschappelijke kans: weer product, maar dit klopt dus niet. Ik zou 36/270725 volgens het boek moeten uitkomen. Waar zit de fout?

Alvast vooraf bedankt (:

Groetjes

Nagare
3de graad ASO - zaterdag 23 mei 2009

Antwoord

Die 'welbepaalde redering' lijkt me nogal onzin! Dat er bij de eerste poging een 'goed' antwoord uitkomt doet vermoeden dat dit geheel gebaseerd is op toeval!

Dit is wel een 'goede' redenering:

Voor de 1e kaart heb je 13 mogelijke gunstige kandidaten (13 schoppen kaarten). Bij de tweede 12, de derde 11 en bij de vierde 10 mogelijkheden. In totaal zijn er 52·51·50·49 mogelijkheden om 4 kaarten uit 52 te kiezen. We zeggen dan:



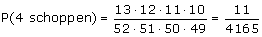
Een andere goede redenering zou zijn dat je zegt dat de kans dat de 1e kaart een schoppen is is 13/52, de kans dat de tweede kaart een schoppen is is 12/51, enz.



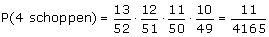
Als je goed kijkt dan zie je dat dat hetzelfde is.

Een andere manier om dit aan te pakken is door gebruik te maken van combinaties. Op hoeveel manieren kan je 4 schoppen kiezen uit 13? En op hoeveel manieren kan je 4 kaarten kiezen uit 52. Je let daarbij verder niet op de volgorde. Dat zou dat dit worden:



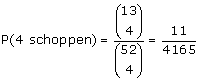
Je kunt bij de laatste ook nog wel even controleren dat dit ook weer 'hetzelfde' is als je bedenkt wat zo'n combinatie ook alweer was.



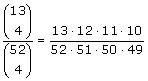
Dat komt me bekend voor...

We hebben dus nu zelfs 3 verschillende (maar dan toch eigenlijk wel een beetje hetzelfde) methodes om dit soort problemen aan te pakken. Ik stel voor dat je dat maar 's eerst probeert voor de tweede opdracht. Je kunt dat als reactie op deze vraag doen en dan zien we wel verder...

Zie ook 1. Eén vraag - drie uitwerkingen

zondag 24 mei 2009

©2001-2024 WisFaq