Riemann-integratie (ondersom)
We hebben maandag examen en onderstaande oefening lukt maar niet:
f(x) = 1/2x2+1
h = 1/2
bereken de ondersom in [0,4]
dank bij voorbaat
Aje vl
3de graad ASO - vrijdag 6 december 2002
Antwoord
Beste Aje,
Ik neem aan dat je met h = 1/2 bedoelt : de breedte van elk deelinterval?
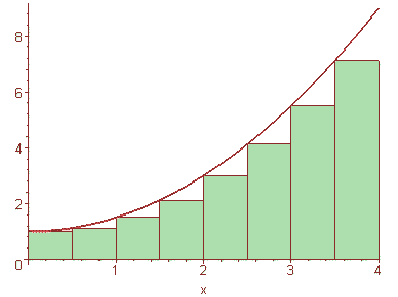
Er zijn dus in totaal 8 deelintervallen ( (4 – 0)/x = 1/2 Û x = 8) te weten : [0, 1/2], [1/2, 1], [1,11/2], [11/2, 2], [2,21/2], [21/2, 3], [3, 31/2], [31/2, 4].Nu neem je de linkerwaarde van het deelinterval en vult deze in de functie in.
Dus voor het eerste interval is de hoogte f(0) = 1, voor het tweede f(1/2) = 9/8, … f(31/2) = 7,125. De benaderde oppervlakte is dus 1/2(f(0) + f(1/2) + f(1) + f(11/2) + f(2) + f(21/2) + f(3) + f(31/2)).
Dus 1/2(1 + 1,125 + 1,5 + 2,125 + 3 + 4,125 + 5,5 + 7,125) = 12,75.
Begrijp je die 1/2? Je berekent namelijk eerst de oppervlakte van elk rechthoekje. En je telt daarna alle oppervlakten van de rechthoekjes op. De breedte van ieder rechthoekje bedraagt 1/2 en vermenigvuldigd met de corresponderende functiewaarde (linkergrens) krijg je de oppervlakte van het desbetreffende rechthoekje (oppervlakte rechthoek is namelijk breedte x hoogte). Omdat elk rechthoekje de breedte 1/2 heeft, mag je die buiten haakjes zetten (door de distributieve eigenschap vermenigvuldig je toch weer met 1/2). Je mag natuurlijk ook 1/2f(0) + 1/2f(1/2) + 1/2f(1) + … opschrijven, maar de vorige manier rekent sneller.
Nu is deze methode nog te doen aangezien er “weinig” deelintervallen zijn, maar indien er veel deelintervallen zijn, is het handiger om het sommatieteken te gebruiken.
In dit geval is de sommatie:  .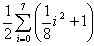
Des te meer deelintervallen je neemt, des te nauwkeuriger de oppervlakte onder de kromme wordt benaderd. De werkelijke waarde van de oppervlakte onder de kromme f(x) = 1/2x2 + 1 op het interval [0,4] is 14,66666… dus 14 2/3.
Ik hoop dat het nu wel duidelijk is, anders mail je maar terug.
vrijdag 6 december 2002
©2001-2024 WisFaq
|
Re: Riemann-integratie (ondersom)