Re: Re: Exterior naar interior mappen

Dit is een reactie op vraag 57025

Ik dacht dat de inversie 1/v gold voor de eenheids cirkel met centrum (0,0). daarnaast heb ik in de eerste stap ook alleen nog het exterior van de cirkel.

Verder was ik eerder door wisfaq verteld dat ik eerst moest kwadrateren en dan pas de straal veranderen. Opzich vond ik dit wel logisch want als we z schrijven als z=rexp(i theta) = exp(i theta) (aangezien r=1 in het begin)
dan geeft kwadrateren z=exp(2i theta) en wat er inderdaad voor zorgt dat het exterior 2x naar het interior wordt gemapt. Als we echter eerst met pi vermenigvuldigen en dan kwadrateren geeft dit z=pi^2exp(2 i theta) wat overduidelijk niet correct is. Echter iedereen die ik over dit probleem gesproken heb krijgt het antwoord 1/(pi^2(z-2)^2)+i wat me nogal verwart.

Overigens heb ik mijn eigen antwoord ook herzien (maar het is nog steeds niet wat de anderen krijgen):

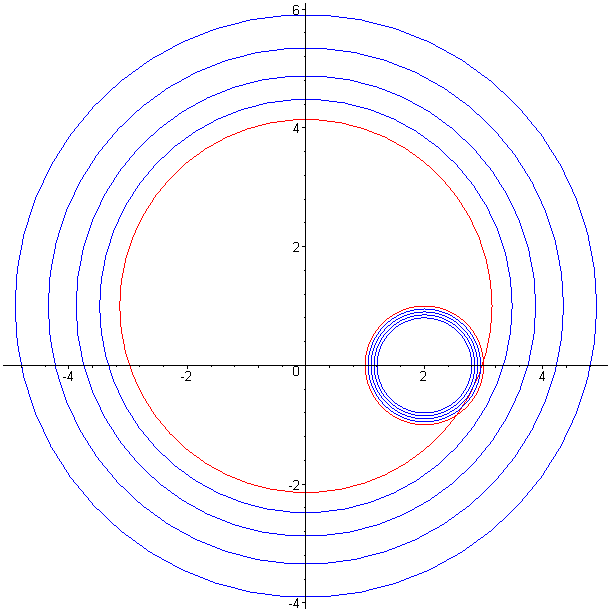
Laat C_1 : |z-2|=1 en C_2: |z-i|=Pi.

Laat w_1=z-2 (transleert C zodat het de eenheids cirkel met centrum (0,0) is). Dan hebben we |w_1|=1.

Laat w_2=1/w_1. Dit is de inversie. We krijgen |w_2|=1

Laat w_3=w_2^2. Dit geeft |w_3|=1

Laat w_4=pi*w_3. Dit geeft |w_4|=pi

Laat w=w_4+i. Dit geeft |w-i|=pi

Dan is de map van het z-vlak naar het w-vlak als volgt

w_1=z-2
w_2=1/w_1=1/(z-2)
w_3=w_2^2=1/(z-2)^2
w_4=pi * w_3 = pi/(z-2)^2
w=w_4+i = [Pi/(z-2)^2]+i

maar zoals ik al zei is dit niet het antwoord wat anderen krijgen. Ik zie echter geen fouten in mijn redenering.

Herman

herman
Student universiteit - dinsdag 4 november 2008

Antwoord

Ik denk nochtans dat het de enige juiste oplossing is en de afbeelding hieronder lijkt me gelijk te geven (rood geeft een rand aan, de stralen van de "broncirkel" rond z=2 zijn 1.00, 0.95, 0.90, 0.85 en 0.80):

woensdag 5 november 2008

©2001-2024 WisFaq