Exponentiele vergelijking

Hoe los ik de volgende vergelijking op tot de vorm R = ...? Ik kom er niet uit, omdat de R zowel in de exponent als er buiten staat:

(1852R)² = N * 0.74^R

Als ik de beide leden als een logaritme schrijf kan ik de R wel uit de exponent halen, maar staat de andere R in een logaritme (als ik me niet vergis: log(1852²R²) = N * R * log(0.74)) en kom ik er ook niet uit.

De vergelijking is overigens het verband tussen de lichtsterkte van een lichtbron en de zichtbaarheid in zeemijlen (R = zichtbaarheid [ZM], N = I/E = Lichtsterkte [cd] / Verlichtingssterkte [lux]).

Koen
Student hbo - zaterdag 30 november 2002

Antwoord

Als je van beide delen van de vergelijking de logaritme neemt, komt er:
log(1852²R²) = log(N) + R . log(0,74)
eventueel verder:
2log(1852) + 2log(R) = log(N) + R . log(0,74)
Je lost daardoor niet veel op.
Nee, (ook) dit type vergelijking is niet te schrijven als R = functie(zonder R).
Je moet dan echt gebruikmaken van benaderingsmethoden.

Echter bij bekende N (ik heb geen flauw benul hoe groot die waarde in de praktijk
kan zijn), kan je toch wel (bijvoorbeeld door inklemmen) de waarde van R berekenen.

We gaan uit van de vergelijking met logaritmen (je gaf zelf de aanzet).
Is N bijvoorbeeld gelijk aan 10⁸, dan vinden we (met weglaten van wat decimalen):
2log(R) + 0,13R = 8 - 6,5
2log(R) + 0,13R = 1,5
Kiezen we R = 3 dan is het linkerlid gelijk aan: 1,3 (te klein)
Kiezen we R = 4 dan is het linkerlid gelijk aan: 1,7 (te groot)
R ligt dus tussen 3 en 4.
Kies je R = 3,5 dan krijg je links de waarde 1,54 (te groot).
R ligt dus tussen 3 en 3,5, enzovoorts.
Beschik je over een grafische rekenmachine, dan gaat het sneller.
Plot de beide grafieken (die van het linker lid en die van het rechter lid) en bepaal hun snijpunt.



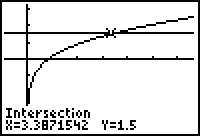
En dan vinden we: X = R = 3,4 (afgerond)

zondag 1 december 2002

©2001-2024 WisFaq