Raaklijnen cirkel zonder gegeven coördinaten

Hallo,

De opgave is:
vind de twee raaklijnen van de cirkel x²+4x+y²+3=0 die gaan door de oorsprong.

Coördinaten middelpunt (-2,0) en de straal 1 zijn makkelijk te vinden na het completeren van het kwadraat:
(x+2)² + y² = 1
Impliciet differentiëren geeft mij voor dy/dx:
2(x+2) + 2y(dy/dx)=0
dy/dx= -(x+2)/y

Uit een schets op papier en met de Plane Graphic Calculator http://www.accesscom.com/~lillge/pgc/
met f=(cos t + Ö(-1) sin t)-2 en voor de raaklijn
g= -x/Ö3 of x/Ö3 valt eenvoudig af te lezen dat het antwoord van het handboek: Ö(y)+x=0 en Ö(y)-x=0), correct is voor bijv. x = 1,5 maar hoe loopt de weg ernaartoe?

Het probleem waar ik mee worstel is dat de coördinaten waarover ik beschik, nl. die van de oorsprong, helemaal niet op de cirkel liggen. Hoe kan ik die toch bruikbaar maken om in te passen in de vergelijking die ik bekwam na het impliciet differentiëren?

mvg

Franci
Iets anders - zaterdag 26 april 2008

Antwoord

Waarom moeilijk doen als het makkelijk kan?
Er geldt:



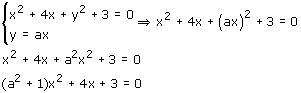
Deze vergelijking zal slecht één oplossing moeten hebben en dat geeft het gevraagde antwoord.

zondag 27 april 2008

©2001-2024 WisFaq