Numeriek differentiëren

Beste WisFaq,
Voor wiskunde moet ik een PO maken waarbij ik het o.a. over numeriek differentiëren moet hebben. Het probleem is alleen dat ik hier ontzettend weinig informatie over kan vinden. Het enige wat ik heb kunnen vinden kwam van hier, maar dit begreep ik alsnog niet echt. Want wat is numeriek differentiëren nou precies en wat voor formules horen daarbij? En zou u misschien ook een voorbeeld erbij kunnen geven met een functie? Want over het algemeen begrijp ik dingen met een voorbeeld meteen :)
Hopelijk beantwoord u mijn vraag!

sanne
Leerling bovenbouw havo-vwo - woensdag 16 april 2008

Antwoord

Een voorbeeld, dat is een goed idee. Laten we nemen y=x², dan weten we uiteraard dat y'=2x. De afgeleide op x=1 is dus y'(1)=2.

Tot zover differentiëren. Als het goed, weet je ook wat de definitie is:



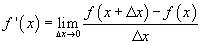
Als je nu numeriek de afgeleide wilt bepalen, dan gaat het je niet lukken met $\Delta x$ naar 0, omdat je dan de waarde van x op twee punten oneindig dicht bij elkaar moet zien te bepalen. Wanneer je nu numeriek differentieert zul je je moeten beperken tot een eindige waarde van $\Delta x$. Omdat hier het functievoorschrift bekend is, kun je de afgeleide benaderen.

Neem bijvoorbeeld $\Delta x$=0.1
y'=[(1+0.1)²-1²]/0.1=2.1
Je ziet dat dat wel redelijk in de buurt komt.

Er zijn wel dingen waar je op moet letten. Je kunt de afgeleide ook zo definiëren. Voor de limiet naar 0 maakt dit niet uit, maar bij eindige $\Delta x$ wel.



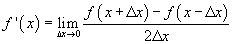
Met steeds een net iets andere uitkomst.

Verder:

• Je kan de numerieke afgeleide makkelijk berekenen in bijvoorbeeld Excel, probeer maar eens.
  
• Hoe zit het met de tweede afgeleide?
  
• Wat is het effect van de grootte van $\Delta x$
  
• Hoe zit dat met minderen elegante functies?
  
• Dit wordt vaak gebruikt om dingen te simuleren. Het gaat dan om differentiaalvergelijkingen.

Bernhard
vrijdag 18 april 2008

Re: Numeriek differentiëren

©2001-2024 WisFaq